题目内容
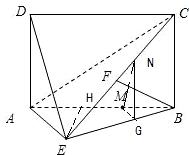
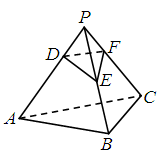
如图,四边形 为矩形,
为矩形, 平面
平面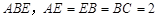 ,
, 为
为 上的点,且
上的点,且 平面
平面 .
.
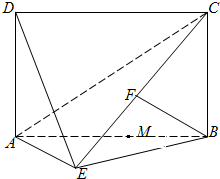
(1)求三棱锥 的体积;
的体积;
(2)设 在线段
在线段 上,且满足
上,且满足 ,试在线段
,试在线段 上确定一点
上确定一点 ,使得
,使得 平面
平面 .
.
 为矩形,
为矩形, 平面
平面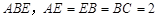 ,
, 为
为 上的点,且
上的点,且 平面
平面 .
. 
(1)求三棱锥
 的体积;
的体积;(2)设
 在线段
在线段 上,且满足
上,且满足 ,试在线段
,试在线段 上确定一点
上确定一点 ,使得
,使得 平面
平面 .
.试题分析:(1)由
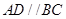 和
和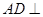 平面
平面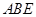 证明
证明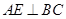 ,再由
,再由 平面
平面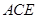 得
得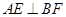 ,根据线面垂直的判定定理证出
,根据线面垂直的判定定理证出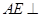 平面
平面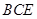 ,得出
,得出 ;由题意知
;由题意知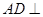 平面
平面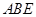 ,则过
,则过 点作
点作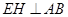 ,得到
,得到 平面
平面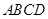 ,再根据条件求出
,再根据条件求出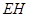 和
和 ,利用换底求出三棱锥的体积;
,利用换底求出三棱锥的体积;(2)根据条件分别在
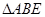 中过
中过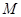 点作
点作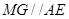 和
和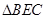 中过
中过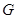 点作
点作 ,根据线面平行的判定证出
,根据线面平行的判定证出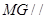 平面
平面 和
和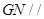 平面
平面 ,由面面平行的判定证出平面
,由面面平行的判定证出平面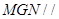 平面
平面 ,则得到
,则得到 点在线段
点在线段 上的位置.
上的位置.试题解析:(1)证明:过
 点作
点作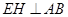 ,
,
∵
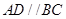 ,
,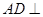 平面
平面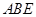
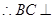 平面
平面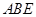
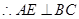
又
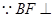 平面
平面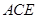
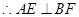

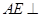 平面
平面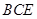 ,且
,且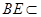 平面
平面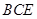 ,
,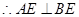
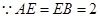
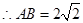 ,
,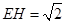
 平面
平面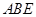
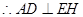
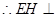 平面
平面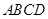
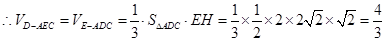
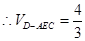
(2)在
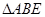 中过
中过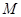 点作
点作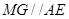 交
交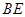 于
于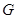 点,在
点,在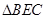 中过
中过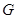 点作
点作 交
交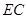 于
于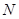 点,连
点,连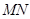 ,
,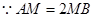
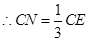
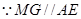 ,
,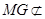 平面
平面 ,
,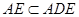
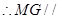 平面
平面
同理可证,
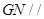 平面
平面
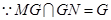
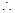 平面
平面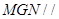 平面
平面
又
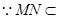 平面
平面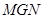 ,
,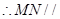 平面
平面
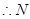 点为线段
点为线段 上靠近
上靠近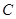 点的一个三等分点
点的一个三等分点
练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案
相关题目
 若将圆锥倒置后,圆锥内水面高为
若将圆锥倒置后,圆锥内水面高为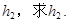
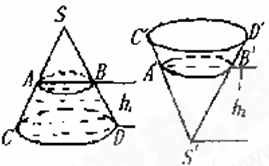
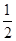 ,AD=1.
,AD=1.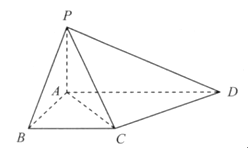
 的底面是边长为1的正六边形,
的底面是边长为1的正六边形, 底面
底面 。
。 平面
平面 ;
;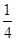 ,求六棱锥
,求六棱锥
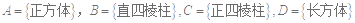 ,它们之间的包含关系是 .
,它们之间的包含关系是 .