题目内容
17.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{3},x≤0}\\{x+\frac{1}{x}-3,x>0}\end{array}\right.$,若关于x的方程f(x2+2x+$\frac{1}{2}$)=m有4个不同的实数根,则m的取值范围是(0,+∞)∪(-1,-$\frac{1}{8}$).分析 令t=x2+2x+$\frac{1}{2}$,则f(t)=m,作出函数f(x)的图象,结合二次方程的判别式的符号,即可判断实根的个数.
解答  解:令t=x2+2x+$\frac{1}{2}$,
解:令t=x2+2x+$\frac{1}{2}$,
则f(t)=m,
由图象可得,当m<-1时,t有一解;
当m=-1时,t有两解;
当-1<m≤0时,t有三解;
当m>0时,t有两解.
当m<-1时,t=x2+2x+$\frac{1}{2}$最多两个根;
当m=-1时,t=±1即x2+2x+$\frac{1}{2}$=±1,方程有两个实根;
当-1<m≤0时,-1<t<1,当-1<t≤$-\frac{1}{2}$,判别式小于等于0,最多一解,有四个根;
当-$\frac{1}{2}$<t≤0时,判别式大于0,有六个根;
当m>0时,即有t>0,t=x2+2x+$\frac{1}{2}$有四个不同的实根,
综上可得m的范围是(0,+∞)∪(-1,-$\frac{1}{8}$).
故答案为:(0,+∞)∪(-1,-$\frac{1}{8}$).
点评 本题考查函数的性质和运用,主要考查函数的零点的判断,注意运用数形结合的思想方法,属于中档题.

练习册系列答案
相关题目
6.设等差数列{an}满足$\frac{si{n}^{2}{a}_{4}-co{s}^{2}{a}_{4}+co{s}^{2}{a}_{4}co{s}^{2}{a}_{8}-si{n}^{2}{a}_{4}si{n}^{2}{a}_{8}}{sin({a}_{5}+{a}_{7})}$=1,公差d∈(-1,0),若当且仅当n=9时,数列{an}的前n项和Sn取得最大值,则首项a1的取值范围是( )
| A. | (π,$\frac{9π}{8}$) | B. | [π,$\frac{9π}{8}$] | C. | [$\frac{7π}{6}$,$\frac{4π}{3}$] | D. | ($\frac{7π}{6}$,$\frac{4π}{3}$) |
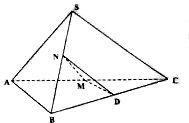 已知三棱锥S-ABC中△SAB与△ABC均为等边三角形,M、N分别为AC、SB的中点,经过M、N且与AB平行的平面α与BC交于点D.
已知三棱锥S-ABC中△SAB与△ABC均为等边三角形,M、N分别为AC、SB的中点,经过M、N且与AB平行的平面α与BC交于点D.