Question

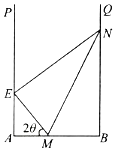
【题目】某地拟在一个U形水面PABQ（∠A=∠B=90°）上修一条堤坝（E在AP上，N在BQ上），围出一个封闭区域EABN，用以种植水生植物．为了美观起见，决定从AB上点M处分别向点E，N拉2条分隔线ME，MN，将所围区域分成3个部分（如图），每部分种植不同的水生植物．已知AB=a，EM=BM，∠MEN=90°，设所拉分隔线总长度为l．

（1）设∠AME=2θ，求用θ表示的l函数表达式，并写出定义域；

（2）求l的最小值．

Answer 1

【答案】（1）l=，θ∈（0，）；（2）lmin=2a．

【解析】

（1）设MN=x，根据AM+BM=a，求出x=,再求得l=，θ∈（0，）；（2）令f（θ）=sinθ（1-sinθ），sinθ∈（0，），利用二次函数的图像和性质求l的最小值．

解：（1）∵EM=BM，∠B=∠MEN，

∴△BMN≌△EMN，

∴∠BNM=∠MNE，

∵∠AME=2θ，

∴∠BNM=∠MNE=θ，

设MN=x，

在△BMN中，BM=xsinθ，∴EM=BM=xsinθ，

∴△EAM中，AM=EMcos2θ=xsinθcos2θ，

∵AM+BM=a，

∴xsinθcos2θ+xsinθ=a，

∴x=，

∴l=EM+MN=，θ∈（0，）；

（2）令f（θ）=sinθ（1-sinθ），sinθ∈（0，），

∴f（θ）≤，

当且仅当θ=时，取得最大值，此时lmin=2a．