题目内容
【题目】冠状病毒是一个大型病毒家族,可引起感冒以及中东呼吸综合征(MERS)和严重急性呼吸综合征(SARS)等较严重疾病.而今年出现在湖北武汉的新型冠状病毒(nCoV)是以前从未在人体中发现的冠状病毒新毒株.人感染了新型冠状病毒后常见体征有呼吸道症状、发热、咳嗽、气促和呼吸困难等.在较严重病例中感染可导致肺炎、严重急性呼吸综合征、肾衰竭,甚至死亡.某医院为筛查冠状病毒,需要检验血液是否为阳性,现有![]() 份血液样本,有以下两种检验方式:
份血液样本,有以下两种检验方式:
方式一:逐份检验,则需要检验![]() 次.
次.
方式二:混合检验,将其中![]() 份血液样本分别取样混合在一起检验,若不是阳性,检验一次就够了,如果检验结果为阳性,为了明确这
份血液样本分别取样混合在一起检验,若不是阳性,检验一次就够了,如果检验结果为阳性,为了明确这![]() 份血液究竟哪几份为阳性,就要对这
份血液究竟哪几份为阳性,就要对这![]() 份再逐份检验,此时这
份再逐份检验,此时这![]() 份血液的检验次数总共为
份血液的检验次数总共为![]() .
.
假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为![]() .现取其中
.现取其中![]() 份血液样本,记采用逐份检验方式,样本需要检验的总次数为
份血液样本,记采用逐份检验方式,样本需要检验的总次数为![]() ,采用混合检验方式,样本需要检验的总次数为
,采用混合检验方式,样本需要检验的总次数为![]() .
.
(1)若![]() ,试求
,试求![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ;
;
(2)若![]() 与干扰素计量
与干扰素计量![]() 相关,其中
相关,其中![]() 是不同的正实数,满足
是不同的正实数,满足![]() 且
且![]() 都有
都有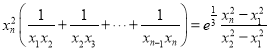 成立.
成立.
(ⅰ)求证:数列![]() 为等比数列;
为等比数列;
(ⅱ)当![]() 时,采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数的期望值更少,求
时,采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数的期望值更少,求![]() 的最大值.
的最大值.
(![]() ,
,![]() )
)
【答案】(1)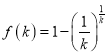 ;(2)(ⅰ)证明见解析;(ⅱ)
;(2)(ⅰ)证明见解析;(ⅱ)![]() 的最大值为4.
的最大值为4.
【解析】
(1)由随机变量的概率公式和数学期望,计算可得所求函数![]() 的解析式;
的解析式;
(2)(ⅰ)当![]() 时可得
时可得![]() ,当
,当![]() 时,可得
时,可得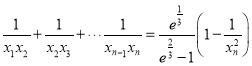 ,
,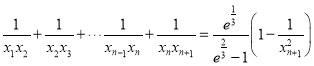 两式作差可得
两式作差可得![]() 即可得证;
即可得证;
(ⅱ)运用(ⅰ)的结论和构造函数,求得导数和单调性,计算可得所求最大值.
解:(1)由已知可得![]() ,
,![]() 的所有取值为1,
的所有取值为1,![]() ,
,![]() ,
,![]()
![]() ,
,
![]() ,
,
由![]() ,可得
,可得![]() ,即
,即![]() ,即
,即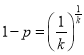 ,即
,即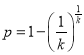 ,
,
可得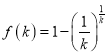 ,
,![]() ,
,![]() ;
;
(2)(ⅰ)证明:当![]() 时,
时,![]() ,即
,即![]() ,由
,由![]() ,得
,得![]() ,
,
因为当![]() 时,
时,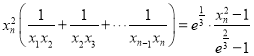 ,
,
所以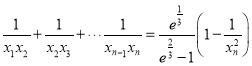 ,
,
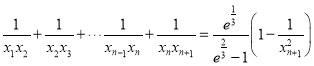
两式相减得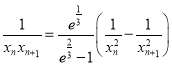 ,
,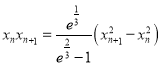
则![]() ,可得
,可得![]() ,因为
,因为![]() ,所以数列
,所以数列![]() 为等比数列,且
为等比数列,且![]() ;
;
(ⅱ)由(ⅰ)可知![]() ,
,![]() ,可得
,可得![]() ,即
,即![]()
![]() ,所以
,所以![]() ,设
,设![]() ,
,![]() ,
,![]() ,当
,当![]() 时,
时,![]() ,
,![]() 递减,又
递减,又![]() ,
,![]() ,则
,则![]() ;
;
![]() ,
,![]() ,则
,则![]() ,可得
,可得![]() 的最大值为4.
的最大值为4.

 名校课堂系列答案
名校课堂系列答案【题目】某公交公司分别推出支付宝和微信扫码支付乘车活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用扫码支付.某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次,用![]() 表示活动推出的天数,
表示活动推出的天数,![]() 表示每天使用扫码支付的人次(单位:十人次),统计数据如表1所示:
表示每天使用扫码支付的人次(单位:十人次),统计数据如表1所示:
表1:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 6 | 11 | 21 | 34 | 66 | 101 | 196 |
根据以上数据,绘制了散点图.
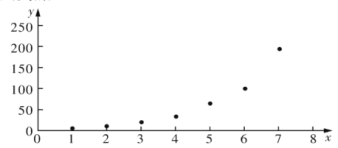
(1)根据散点图判断,在推广期内,![]() 与
与![]() (
(![]() 均为大于零的常数)哪一个适宜作为扫码支付的人次
均为大于零的常数)哪一个适宜作为扫码支付的人次![]() 关于活动推出天数
关于活动推出天数![]() 的回归方程类型?(给出判断即可,不必说明理由).
的回归方程类型?(给出判断即可,不必说明理由).
(2)根据(1)的判断结果及表1中的数据,建立![]() 关于
关于![]() 的回归方程,并预测活动推出第8天使用扫码支付的人次.
的回归方程,并预测活动推出第8天使用扫码支付的人次.
(3)推广期结束后,为更好的服务乘客,车队随机调查了100人次的乘车支付方式,得到如下结果:
表2
支付方式 | 现金 | 乘车卡 | 扫码 |
人次 | 10 | 60 | 30 |
已知该线路公交车票价2元,使用现金支付的乘客无优惠,使用乘车卡支付的乘客享受8折优惠,扫码支付的乘客随机优惠,根据调査结果发现:使用扫码支付的乘客中有5名乘客享受7折优惠,有10名乘客享受8折优惠,有15名乘客享受9折优惠.预计该车队每辆车每个月有1万人次乘车,根据所给数据,以事件发生的频率作为相应事件发生的概率,在不考虑其他因素的条件下,按照上述收费标准,试估计该车队一辆车一年的总收入.
参考数据:
|
|
|
|
|
62.14 | 1.54 | 2535 | 50.12 | 3.47 |
其中![]() .
.
参考公式:
对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: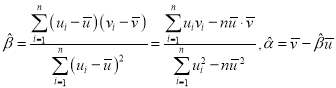 .
.