Question

【题目】已知函数f(x)＝x2－bx＋3.

(1)若f(0)＝f(4)，求函数f(x)的零点；

(2)若函数f(x)一个零点大于1，另一个零点小于1，求b的取值范围．

Answer 1

【答案】（1）1和3 (2) b的取值范围为(4，＋∞)

【解析】试题分析：（1）由，得出，再将代入函数，解方程即可；（2）根据二次函数的图象，只需即可.

试题解析：(1)由f(0)＝f(4)，得3＝16－4b＋3，即b＝4，所以f(x)＝x2－4x＋3，令f(x)＝0，

即x2－4x＋3＝0，得x1＝3，x2＝1，

所以f(x)的零点是1和3.

(2)因为f(x)的零点一个大于1，另一个小于1，如图．

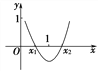
需f(1)<0，即1－b＋3<0，所以b>4.

故b的取值范围为(4，＋∞)．