题目内容
【题目】如图,椭圆![]() :
:![]() (
(![]() )和圆
)和圆![]() :
:![]() ,已知圆
,已知圆![]() 将椭圆
将椭圆![]() 的长轴三等分,椭圆
的长轴三等分,椭圆![]() 右焦点到右准线的距离为
右焦点到右准线的距离为![]() ,椭圆
,椭圆![]() 的下顶点为
的下顶点为![]() ,过坐标原点
,过坐标原点![]() 且与坐标轴不重合的任意直线
且与坐标轴不重合的任意直线![]() 与圆
与圆![]() 相交于点
相交于点![]() 、
、![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 、
、![]() 分别与椭圆
分别与椭圆![]() 相交于另一个交点为点
相交于另一个交点为点![]() 、
、![]() .
.
①求证:直线![]() 经过一定点;
经过一定点;
②试问:是否存在以![]() 为圆心,
为圆心,![]() 为半径的圆
为半径的圆![]() ,使得直线
,使得直线![]() 和直线
和直线![]() 都与圆
都与圆![]() 相交?若存在,请求出实数
相交?若存在,请求出实数![]() 的范围;若不存在,请说明理由。
的范围;若不存在,请说明理由。
【答案】(1)![]() ;(2)①详见解析;②存在,
;(2)①详见解析;②存在,![]() .
.
【解析】
试题(1)由圆C2将椭圆C1的长轴三等分,可得![]() ;又椭圆C1右焦点到右准线的距离为
;又椭圆C1右焦点到右准线的距离为![]() ,可得
,可得![]() ,及a2=b2+c2即可得出;(2)①由题意知直线PE,ME的斜率存在且不为0,设直线PE的斜率为k,则PE:y=kx-1,与椭圆的方程联立可得点P的坐标,同理可得点M的坐标,进而得到直线PM的方程,可得直线PM过定点.
,及a2=b2+c2即可得出;(2)①由题意知直线PE,ME的斜率存在且不为0,设直线PE的斜率为k,则PE:y=kx-1,与椭圆的方程联立可得点P的坐标,同理可得点M的坐标,进而得到直线PM的方程,可得直线PM过定点.
②由直线PE的方程与圆的方程联立可得点A的坐标,进而得到直线AB的方程.假设存在圆心为(m,0),半径为![]() 的圆G,使得直线PM和直线AB都与圆G相交,则圆心到二直线的距离都小于半径
的圆G,使得直线PM和直线AB都与圆G相交,则圆心到二直线的距离都小于半径![]() .即(i)
.即(i)![]() ,(ii)
,(ii)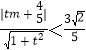 .得出m的取值范围存在即可.
.得出m的取值范围存在即可.
试题解析:(Ⅰ )依题意,![]() ,则
,则![]() ,
,
∴![]() ,又
,又![]() ,∴
,∴![]() ,则
,则![]() ,
,
∴椭圆方程为![]() .
.
(2)①由题意知直线![]() 的斜率存在且不为0,设直线
的斜率存在且不为0,设直线![]() 的斜率为
的斜率为![]() ,则
,则![]() :
:![]() ,
,
由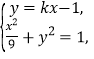 得
得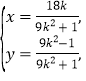 或
或![]()
∴![]() ,
,
用![]() 去代
去代![]() ,得
,得![]() ,
,
方法1: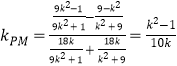 ,
,
∴![]() :
:![]() ,即
,即![]() ,
,
∴直线![]() 经过定点
经过定点![]() .
.
方法2:作直线![]() 关于
关于![]() 轴的对称直线
轴的对称直线![]() ,此时得到的点
,此时得到的点![]() 、
、![]() 关于
关于![]() 轴对称,则
轴对称,则![]() 与
与![]() 相交于
相交于![]() 轴,可知定点在
轴,可知定点在![]() 轴上,
轴上,
当![]() 时,
时,![]() ,
,![]() ,此时直线
,此时直线![]() 经过
经过![]() 轴上的点
轴上的点![]() ,
,
∵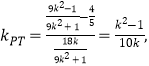
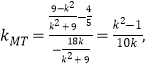
∴![]() ,∴
,∴![]() 、
、![]() 、
、![]() 三点共线,即直线
三点共线,即直线![]() 经过点
经过点![]() ,
,
综上所述,直线![]() 经过定点
经过定点![]() .
.
②由![]() 得
得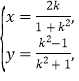 或
或![]() ∴
∴![]() ,
,
则直线![]() :
:![]() ,
,
设![]() ,则
,则![]() ,直线
,直线![]() :
:![]() ,直线
,直线![]() :
:![]() ,
,
假设存在圆心为![]() ,半径为
,半径为![]() 的圆
的圆![]() ,使得直线
,使得直线![]() 和直线
和直线![]() 都与圆
都与圆![]() 相交,
相交,
则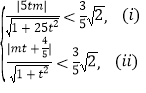 由(
由(![]() )得
)得![]() 对
对![]() 恒成立,则
恒成立,则![]() ,
,
由(![]() )得,
)得,![]() 对
对![]() 恒成立,
恒成立,
当![]() 时,不合题意;当
时,不合题意;当![]() 时,
时,![]() ,得
,得![]() ,即
,即![]() ,
,
∴存在圆心为![]() ,半径为
,半径为![]() 的圆
的圆![]() ,使得直线
,使得直线![]() 和直线
和直线![]() 都与圆
都与圆![]() 相交,所有
相交,所有![]() 的取值集合为
的取值集合为![]() .
.
解法二:圆![]() ,由上知
,由上知![]() 过定点
过定点![]() ,故
,故![]() ;又直线
;又直线![]() 过原点,故
过原点,故![]() ,从而得
,从而得![]() .
.

 黄冈创优卷系列答案
黄冈创优卷系列答案【题目】某商店为了更好地规划某种商品进货的量,该商店从某一年的销售数据中,随机抽取了![]() 组数据作为研究对象,如下图所示(
组数据作为研究对象,如下图所示(![]() (吨)为该商品进货量,
(吨)为该商品进货量, ![]() (天)为销售天数):
(天)为销售天数):
| 2 | 3 | 4 | 5 | 6 | 8 | 9 | 11 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
(Ⅰ)根据上表数据在下列网格中绘制散点图;
(Ⅱ)根据上表提供的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅲ)在该商品进货量![]() (吨)不超过6(吨)的前提下任取两个值,求该商品进货量x(吨)恰有一个值不超过3(吨)的概率.
(吨)不超过6(吨)的前提下任取两个值,求该商品进货量x(吨)恰有一个值不超过3(吨)的概率.
参考公式和数据: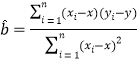 ,
,![]() .
.![]()
