题目内容
18.已知f(x)是定义在R上奇函数,又f(2)=0,若x>0时,xf′(x)+f(x)>0,则不等式xf(x)<0的解集是(-2,0)U(0,2).分析 由题意可得F(x)=xf(x)为R上偶函数,且在(0,+∞)单调递增,在(-∞,0)单调递减,不等式xf(x)<0等价于F(x)<F(2),结合函数的性质可得.
解答 解:∵f(x)是定义在R上奇函数,
∴F(x)=xf(x)为R上偶函数,
又f(2)=0,∴F(2)=0,
∵x>0时,xf′(x)+f(x)>0,
∴x>0时,F′(x)=xf′(x)+f(x)>0,
∴函数F(x)在(0,+∞)单调递增,在(-∞,0)单调递减,
不等式xf(x)<0等价于F(x)<0,即F(x)<F(2),
由单调性可得2<x<2,
又F(0)=0,不满足F(x)<F(2),
故所求解集为(-2,0)U(0,2)
故答案为:(-2,0)U(0,2)
点评 本题考查导数的运算,涉及构造函数以及利用函数的单调性和奇偶性求解不等式,属中档题.

练习册系列答案
相关题目
9.在如图的知识结构图中:“求简单函数的导数”的“上位”要素有( )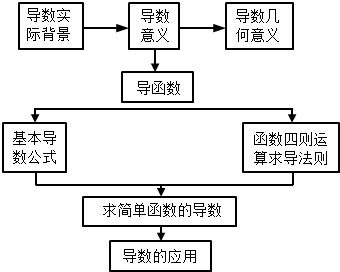

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.等边三角形ABC的边长是a,AD是BC边上的高,沿AD将△ABC折成直二面角,则点B、C的距离是( )
| A. | $\frac{1}{2}$a | B. | $\frac{\sqrt{2}}{2}$a | C. | $\frac{\sqrt{3}}{2}$a | D. | a |
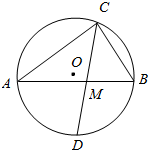 如图,已知AB是⊙O的直径,C为圆上一点,连接CB、AC,点D是半圆弧AB的中点,若圆的半径为4,DC交AB于M点,则DM•DC的范围是32.
如图,已知AB是⊙O的直径,C为圆上一点,连接CB、AC,点D是半圆弧AB的中点,若圆的半径为4,DC交AB于M点,则DM•DC的范围是32.