题目内容

10．等边三角形ABC的边长是a，AD是BC边上的高，沿AD将△ABC折成直二面角，则点B、C的距离是（　　）
A．$\frac{1}{2}$aB．$\frac{\sqrt{2}}{2}$aC．$\frac{\sqrt{3}}{2}$aD．a

分析 利用二面角确定∠BDC=90°，画出图形，通过求解三角形即可得到结果．

解答 解：如图，因为AD是正△ABC的高线，所以∠BDC即为二面角的平面角，即∠BDC=90°，
等边三角形ABC的边长为a，
因为CD=BD=$\frac{a}{2}$，所以BC=$\frac{\sqrt{2}a}{2}$，
故选：B．

点评 本题考查面面角，考查空间距离的计算，属于基础题．

练习册系列答案
相关题目
12．已知集合A={x|x2-2x+1＜a2}，B={x|-1＜x＜2}，若A⊆B，则正实数a的取值范围为（　　）
A．（1，+∞）B．（1，2]C．（0，1]D．（0，2]
1．已知$\overrightarrow a=（-3，2），\overrightarrow b=（-1，-1）$，向量λ$\overrightarrow a+\overrightarrow b$与$\overrightarrow a-2\overrightarrow b$垂直，则实数λ的值为（　　）
A．$-\frac{1}{2}$B．$\frac{3}{11}$C．$\frac{1}{6}$D．$\frac{1}{7}$
18．已知f（x）是定义在R上奇函数，又f（2）=0，若x＞0时，xf′（x）+f（x）＞0，则不等式xf（x）＜0的解集是（-2，0）U（0，2）．
5．函数y=sin（ωx+φ）的部分图象如图，则f（$\frac{π}{2}$）=（　　）
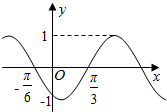
A．-$\frac{1}{2}$B．$\frac{1}{2}$C．-$\frac{\sqrt{3}}{2}$D．$\frac{\sqrt{3}}{2}$
15．已知f（x）为R上的奇函数，当x＞0时，f（x）=x2+2x+8，则f（x）的解析式为$f（x）=\left\{\begin{array}{l}-{x^2}+2x-8，x＜0\\ 0，x=0\\{x^2}+2x+8，x＞0\end{array}\right.$．
2．已知圆N：（x+1）2+y2=2的切线l与抛物线C：y2=x交于不同的两点A，B．
（1）当切线l斜率为-1时，求线段AB的长；
（2）设点M和点N关于直线y=x对称，且$\overrightarrow{MA}$•$\overrightarrow{MB}$=0，求直线l的方程．
19．已知函数y=f（x），x∈F．集合A={（x，y）|y=f（x），x∈F}，B={（x，y）|x=1}，则A∩B中所含元素的个数是（　　）
A．.0B．.1C．.0或1D．.1或2
20．函数f（x）=log3x对任意正数x，y都成立的结论有（　　）
①f（x+y）=f（x）f（y）
②f（x+y）=f（x）+f（y）
③f（xy）=f（x）f（y）
④f（xy）=f（x）+f（y）
A．②B．④C．①④D．②③

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网