题目内容
1.若实数x1,x2,y1,y2满足${(2si{nx}_{1}{-y}_{1})}^{2}$+${{(x}_{2}{-y}_{2}+\sqrt{3})}^{2}$=0(0<x1<π),则${{(x}_{1}{-x}_{2})}^{2}{+{(y}_{1}{-y}_{2})}^{2}$的最小值是( )| A. | $\frac{{π}^{2}}{18}$ | B. | $\frac{{π}^{2}}{9}$ | C. | $\frac{\sqrt{2}}{6}π$ | D. | $\frac{π}{9}$ |
分析 化简已知条件,得到两个函数,利用函数的导数求出切线的斜率,利用平行线之间的距离求解即可.
解答 解:实数x1,x2,y1,y2满足${(2si{nx}_{1}{-y}_{1})}^{2}$+${{(x}_{2}{-y}_{2}+\sqrt{3})}^{2}$=0(0<x1<π),
可得y1=2sinx1,并且x2-y2+$\sqrt{3}$=0,(x1-x2)2+(y1-y2)2的最小值转化为:函数y=2sinx图象上的点与x-y+$\sqrt{3}$=0图象上的点的距离的最小值,
由y=2sinx可得y′=2cosx.与直线x-y+$\sqrt{3}$=0平行的直线的斜率为1,所以2cosx=1,
因为0<x<π,所以解得x=$\frac{π}{3}$,
切点坐标($\frac{π}{3}$,$\sqrt{3}$),与x-y+$\sqrt{3}$=0平行的直线为:y-$\sqrt{3}$=x-$\frac{π}{3}$,即x-y+$\sqrt{3}$-$\frac{π}{3}$=0
(x1-x2)2+(y1-y2)2的最小值为:$\frac{\frac{π}{3}}{\sqrt{2}}$=$\frac{\sqrt{2}}{6}π$.
故选:C.
点评 本题考查函数与方程的综合应用,函数的导数求解函数的最值,考查计算能力以及转化思想.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
13.设等差数列{an}的公差是d,其前项和是Sn,若a1=d=1,则$\frac{{S}_{n}+8}{{a}_{n}}$的最小值是( )
| A. | $\frac{9}{2}$ | B. | $\frac{7}{2}$ | C. | 2$\sqrt{2}$+$\frac{1}{2}$ | D. | 2$\sqrt{2}$-$\frac{1}{2}$ |
10.已知x∈{1,2,x2},则有( )
| A. | x=1 | B. | x=1或x=2 | C. | x=0或x=2 | D. | x=0或x=1或x=2 |
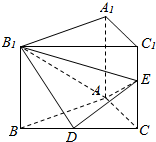 如图,在直三棱柱ABC-A1B1C1中,D,E分别是BC和CC1的中点,已知AB=AC=AA1=4,∠BAC=90°.
如图,在直三棱柱ABC-A1B1C1中,D,E分别是BC和CC1的中点,已知AB=AC=AA1=4,∠BAC=90°.