题目内容
6. 如图,在四棱锥A-DCBE中,AC⊥BC,底面DCBE为平行四边形,DC⊥平面ABC.
如图,在四棱锥A-DCBE中,AC⊥BC,底面DCBE为平行四边形,DC⊥平面ABC.(Ⅰ)求证:DE⊥平面ACD;
(Ⅱ)若∠ABC=30°,AB=2,EB=$\sqrt{3}$,求三棱锥B-ACE的体积;
(Ⅲ)设平面ADE∩平面ABC=直线l,求证:BC∥l.
分析 (Ⅰ)利用线面垂直的判定定理证明BC⊥平面ACD,利用底面DCBE为平行四边形,所以BC∥ED,可得DE⊥平面ACD;
(Ⅱ)证明BE⊥平面ABC,利用VB-ACE=VE-ABC,求三棱锥B-ACE的体积;
(Ⅲ)证明BC∥平面ADE,利用平面ADE∩平面ABC=直线l,可得BC∥l.
解答 (Ⅰ)证明:因为DC⊥平面ABC,BC?平面ABC,所以BC⊥DC.…(1分)
又因为AC⊥BC,AC?平面ACD,CD?平面ACD,AC∩CD=C,
所以,BC⊥平面ACD.…(3分)
因为底面DCBE为平行四边形,所以BC∥ED.
所以DE⊥平面ACD.…(5分)
(Ⅱ)解:因为底面DCBE为平行四边形,DC⊥平面ABC,
所以BE⊥平面ABC.
所以VB-ACE=VE-ABC=$\frac{1}{3}×\frac{1}{2}×1×\sqrt{3}×\sqrt{3}=\frac{1}{2}$.…(8分)
(Ⅲ)证明:因为底面DCBE为平行四边形,所以BC∥ED.…(9分)
因为BC?平面ADE,ED?平面ADE,所以BC∥平面ADE.…(10分)
因为,平面ADE∩平面ABC=l,BC?平面ABC,所以BC∥l.…(12分)
点评 本题考查线面垂直的判定,考查线面平行,三棱锥体积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
11.在半径为10cm的球面上有A,B,C三点,如果AB=8$\sqrt{3}$,∠ACB=60°,则球心O到平面ABC的距离为( )
| A. | 2cm | B. | 4cm | C. | 6cm | D. | 8cm |
16.设直线y=k(x-4)+3是圆x2+y2=9的一条割线,则k的取值一定满足( )
| A. | (-∞,-$\frac{24}{7}$) | B. | (0,$\frac{24}{7}$) | C. | (-$\frac{24}{7}$,0) | D. | (-$\frac{24}{7}$,$\frac{24}{7}$) |
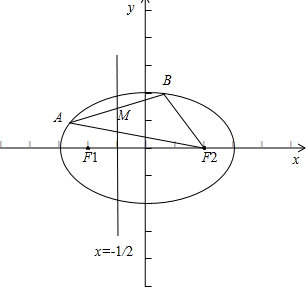 如图,F1,F2是椭圆C:$\frac{{x}^{2}}{2}$+y2=1的左、右焦点,A,B是椭圆C上的两个动点,且线段AB的中点M在直线l:x=-$\frac{1}{2}$上.
如图,F1,F2是椭圆C:$\frac{{x}^{2}}{2}$+y2=1的左、右焦点,A,B是椭圆C上的两个动点,且线段AB的中点M在直线l:x=-$\frac{1}{2}$上. 如图,平面PAC⊥平面ABC,AC⊥BC,△PAC为等边三角形,PE∥CB,M,N分别是线段AE,AP上的动点,且满足:$\frac{AM}{AE}$=$\frac{AN}{AP}$=λ(0<λ<1).
如图,平面PAC⊥平面ABC,AC⊥BC,△PAC为等边三角形,PE∥CB,M,N分别是线段AE,AP上的动点,且满足:$\frac{AM}{AE}$=$\frac{AN}{AP}$=λ(0<λ<1).
 如图,在四面体ABCD中,平面BAD⊥平面CAD,∠BAD=90°.M,N,Q分别为棱AD,BD,AC的中点.
如图,在四面体ABCD中,平面BAD⊥平面CAD,∠BAD=90°.M,N,Q分别为棱AD,BD,AC的中点.