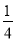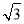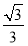Question

某镇政府为了更好地服务于农民，派调查组到某村考察．据了解，该村有100户农民，且都从事蔬菜种植，平均每户的年收入为3万元．为了调整产业结构，该镇政府决定动员部分农民从事蔬菜加工．据估计，若能动员x(x＞0)户农民从事蔬菜加工，则剩下的继续从事蔬菜种植的农民平均每户的年收入有望提高2x%，而从事蔬菜加工的农民平均每户的年收入将为3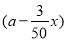 (a＞0)万元．

(1)在动员x户农民从事蔬菜加工后，要使从事蔬菜种植的农民的总年收入不低于动员前从事蔬菜种植的农民的总年收入，求x的取值范围；

(2)在(1)的条件下，要使这100户农民中从事蔬菜加工的农民的总年收入始终不高于从事蔬菜种植的农民的总年收入，求a的最大值．

 

Answer 1

（1）0＜x≤50（2）5

【解析】(1)由题意，得3(100－x)(1＋2x%)≥3×100，

即x2－50x≤0，又x＞0，解得0＜x≤50.

(2)从事蔬菜加工的农民总年收入为3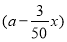x万元，

从事蔬菜种植的农民的总年收入为3(100－x)(1＋2x%)万元．

根据题意，得3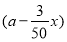x≤3(100－x)(1＋2x%)恒成立，

即ax≤100＋x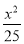＋恒成立．

因为0＜x≤50，所以a≤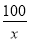＋＋1恒成立，

而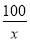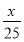＋＋1≥5，当且仅当x＝50时取等号，所以a的最大值为5.