题目内容
若曲线y＝2x2的一条切线l与直线x＋4y－8＝0垂直，则切线l的方程为( )．
A．x＋4y＋3＝0 B．x＋4y－9＝0
C．4x－y＋3＝0 D．4x－y－2＝0
D
【解析】y′＝4x，设切点M(x0，y0)，∴k＝4x0.又∵x＋4y－8＝0的斜率k1＝
－
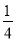，∴k＝4x0＝4，x0＝1，y0＝2
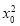＝2，即切点为M(1,2)，k＝4.故切线l的方程为y－2＝4(x－1)，即4x－y－2＝0，故选D.
练习册系列答案
相关题目
题目内容
若曲线y＝2x2的一条切线l与直线x＋4y－8＝0垂直，则切线l的方程为( )．
A．x＋4y＋3＝0 B．x＋4y－9＝0
C．4x－y＋3＝0 D．4x－y－2＝0
D
【解析】y′＝4x，设切点M(x0，y0)，∴k＝4x0.又∵x＋4y－8＝0的斜率k1＝
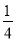－，∴k＝4x0＝4，x0＝1，y0＝2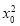＝2，即切点为M(1,2)，k＝4.故切线l的方程为y－2＝4(x－1)，即4x－y－2＝0，故选D.
