题目内容
【题目】如图，设椭圆 
+ 
=1（a＞b＞0）的左右焦点分别为F1 ， F2 ， 点D在椭圆上，DF1⊥F1F2 ， 
=2 
，△DF1F2的面积为 
． （Ⅰ）求该椭圆的标准方程；
（Ⅱ）是否存在圆心在y轴上的圆，使圆在x轴的上方与椭圆有两个交点，且圆在这两个交点处的两条切线互相垂直并分别过不同的焦点？若存在，求出圆的方程；若不存在，请说明理由．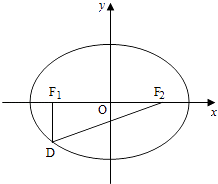
【答案】解：（Ⅰ）设F1（﹣c，0），F2（c，0），其中c2=a2﹣b2 ， 由 
=2 
，得|DF1|= 
= 
c，
从而 
= 
|DF1||F1F2|= c2= ，故c=1．
从而|DF1|= ，由DF1⊥F1F2 ， 得 
= 
+ 
= 
，
因此|DF2|= 
，
所以2a=|DF1|+|DF2|=2 ，故a= ，b2=a2﹣c2=1，
因此，所求椭圆的标准方程为 
+y2=1；
（Ⅱ）设圆心在y轴上的圆C与椭圆 +y2=1相交，P1（x1 ， y1），P2（x2 ， y2）是两个交点，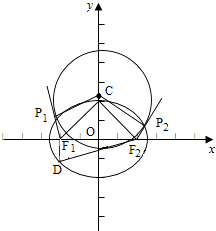
y1＞0，y2＞0，F1P1 ， F2P2是圆C的切线，且F1P1⊥F2P2 ， 由圆和椭圆的对称性，易知x2=﹣x1 ， y1=y2 ， |P1P2|=2|x1|，
由（Ⅰ）知F1（﹣1，0），F2（1，0），所以 
=（x1+1，y1）， 
=（﹣x1﹣1，y1），再由F1P1⊥F2P2 ， 得﹣ 
+ 
=0，
由椭圆方程得1﹣ 
= ，即3 
+4x1=0，解得x1=﹣ 
或x1=0．
当x1=0时，P1 ， P2重合，此时题设要求的圆不存在；
当x1=﹣ 时，过P1 ， P2 ， 分别与F1P1 ， F2P2垂直的直线的交点即为圆心C，设C（0，y0）
由F1P1 ， F2P2是圆C的切线，知CP1⊥F1P1 ， 得 
=﹣1，而|y1|=|x1+1|= 
，
故y0= 
，
故圆C的半径|CP1|=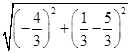 
= 
．
综上，存在满足题设条件的圆，其方程为x2+ 
= 
【解析】（Ⅰ）设F1（﹣c，0），F2（c，0），依题意，可求得c=1，易求得|DF1|= 
= 
，|DF2|= 
，从而可得2a=2 
，于是可求得椭圆的标准方程；（Ⅱ）设圆心在y轴上的圆C与椭圆 
+y2=1相交，P1（x1 ， y1），P2（x2 ， y2）是两个交点，依题意，利用圆和椭圆的对称性，易知x2=﹣x1 ， y1=y2 ， |P1P2|=2|x1|，由F1P1⊥F2P2 ， 得x1=﹣ 
或x1=0，分类讨论即可求得圆心及半径，从而可得的方程．
