题目内容
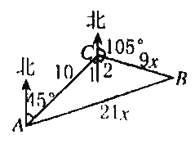
【题目】在亚丁湾海域执行护航任务的中国海军“徐州”舰,在A处收到某商船在航行中发出求救信号后,立即测出该商船在方位角方位角(是从某点的指北方向线起,依顺时针方向到目标方向线之间的水平夹角)为45°、距离A处为10 n mile的C处,并测得该船正沿方位角为105°的方向,以9 n mile/h的速度航行,“徐州”舰立即以21 n mile/h的速度航行前去营救.
(1)“徐州”舰最少需要多少时间才能靠近商船?
(2)在营救时间最少的前提下,“徐州”舰应按照怎样的航行方向前进?(角度精确到0.1°,时间精确到1min,参考数据:sin68.2°≈0.9286)
【答案】(1)最少需要40min才能靠近商船;(2)前进的方位角约为![]() .
.
【解析】
(1) 由题知舰艇沿直线航行时所需时间最少,设舰艇在B处靠近商船,从A处到靠近商船所用的时间为x h.根据余弦定理,可得![]() ,解方程即得x的值,即得“徐州”舰最少需要多少时间才能靠近商船.(2)由余弦定理可得
,解方程即得x的值,即得“徐州”舰最少需要多少时间才能靠近商船.(2)由余弦定理可得![]() 大小,再求“徐州”舰前进的方位角.
大小,再求“徐州”舰前进的方位角.
(1)由题知舰艇沿直线航行时所需时间最少,设舰艇在B处靠近商船,从A处到靠近商船所用的时间为x h.
则![]() ,
,![]() ,
,
![]() .
.
又![]() ,
,
根据余弦定理,可得
![]() ,即
,即
![]() ,
,
即![]() ,
,
解得![]() ,
,![]() (舍去).
(舍去).
故“徐州”舰最少需要40min才能靠近商船.
(2)由(1)知![]() ,
,![]() ,
,
由余弦定理可得![]() ,
,
![]() ,
,
故“徐州”舰前进的方位角约为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目