题目内容
13.设奇函数f(x)满足f(x)=log2x-1(x>0),则{x|f(x+1)>0}=( )| A. | {x|x<-2或x>2} | B. | {x|-2<x<0或x>3} | C. | {x|x<-3或-1<x<1} | D. | {x|-3<x<-1或x>1} |
分析 由函数解析式结合函数图象平移作出函数f(x)的图象及f(x+1)的图象,数形结合求得{x|f(x+1)>0}.
解答 解:∵函数f(x)为奇函数,且f(x)=log2x-1(x>0),
设x<0,则-x>0,
∴f(x)=-f(-x)=-[log2(-x)-1]=-log2(-x)+1.
分别作出函数f(x)和f(x+1)的图象如图: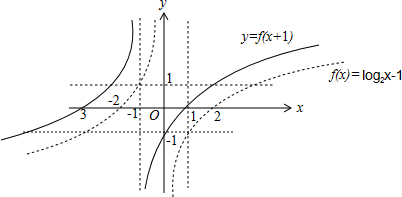
由图可知:{x|f(x+1)>0}={x|-3<x<-1或x>1}.
故选:D.
点评 本题考查函数的性质及其应用,考查了对数不等式的解法,体现了数形结合的解题思想方法,是中档题.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目