题目内容
【题目】数列![]() 的前n项和记为
的前n项和记为![]() ,
,![]() ,数列
,数列![]() 满足
满足![]() :
:
(1)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)数列![]() 满足
满足![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() ;
;
(3)若![]() 对任意正整数n都成立,求实数x的取值范围.
对任意正整数n都成立,求实数x的取值范围.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由![]() 可得
可得![]() 是等比数列,公比是-2,首项为1,由此可求出
是等比数列,公比是-2,首项为1,由此可求出![]() 的通项公式,再对
的通项公式,再对![]() 化简变形即可求出
化简变形即可求出![]() 的通项公式;(2)根据错位相减法求出数列
的通项公式;(2)根据错位相减法求出数列![]() 的前n项和
的前n项和![]() 即可;(3)令
即可;(3)令![]() ,利用作差法
,利用作差法![]() 研究单调性,分析可知
研究单调性,分析可知![]() ,从而解不等式
,从而解不等式![]() 即可求得结果.
即可求得结果.
(1)∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
两式相减,则![]() ,即
,即![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ∴
∴![]() ,
,
∴![]() 是等比数列,公比是-2,首项为1,
是等比数列,公比是-2,首项为1,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ;
;
(2)∵![]() ∴
∴![]() ,
,
∴![]() ,
,
![]() ,
,
两式相减得![]()
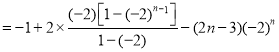
![]()
![]() .
.
∴![]() ;
;
(3)令![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,∴
,∴![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() ,∴
,∴![]() 即
即![]() ,
,
当![]() 时,
时,![]() ,∴
,∴![]() ,
,
∴![]() …,
…,
∴当![]() 时,
时,![]() .
.
∵![]() 对任意正整数n都成立,
对任意正整数n都成立,
∴![]() ,
,
解得![]() .
.
所以实数x的取值范围是![]() .
.

【题目】某企业生产的某种产品被检测出其中一项质量指标存在问题.该企业为了检查生产该产品的甲、乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.如图是甲流水线样本的频数分布表和乙流水线样本的频率分布直方图.
内,则为合格品,否则为不合格品.如图是甲流水线样本的频数分布表和乙流水线样本的频率分布直方图.
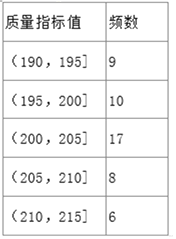
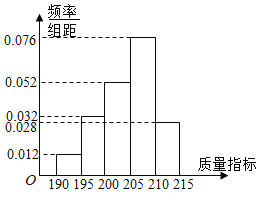
(1)根据频率分布直方图,估计乙流水线生产的产品该质量指标值的中位数;
(2)若将频率视为概率,某个月内甲、乙两条流水线均生产了5000件产品,则甲、乙两条流水线分别生产出不合格品约多少件?
(3)根据已知条件完成下面![]() 列联表,并回答是否有
列联表,并回答是否有![]() 的把握认为“该企业生产的这种产品的质量指标值与甲、乙两条流水线的选择有关”?
的把握认为“该企业生产的这种产品的质量指标值与甲、乙两条流水线的选择有关”?
甲流水线 | 乙流水线 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
附:![]() ,其中
,其中![]() .
.
临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |