题目内容
已知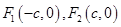 分别是椭圆
分别是椭圆 的左、右焦点,椭圆的离心率
的左、右焦点,椭圆的离心率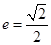 .
.
(I)求椭圆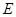 的方程;(II)已知直线
的方程;(II)已知直线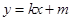 与椭圆
与椭圆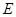 有且只有一个公共点
有且只有一个公共点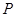 ,且与直线
,且与直线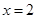 相交于点
相交于点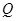 .求证:以线段
.求证:以线段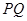 为直径的圆恒过定点
为直径的圆恒过定点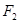 .
.
(I)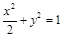 ;(II)详见试题解析.
;(II)详见试题解析.
解析试题分析:(I)由题意可知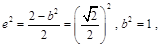 从而可得椭圆
从而可得椭圆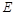 的方程;(II)由(I)知
的方程;(II)由(I)知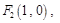 联立动直线和椭圆方程可得:
联立动直线和椭圆方程可得: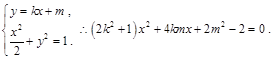 再利用向量数量积的坐标公式及韦达定理通过计算证明结论.
再利用向量数量积的坐标公式及韦达定理通过计算证明结论.
试题解析:(I)解:由题意可知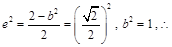 椭圆
椭圆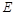 的方程为
的方程为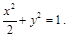 4分
4分
(II)证明:由(I)知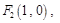 联立动直线和椭圆方程可得:
联立动直线和椭圆方程可得: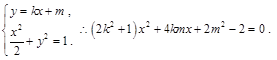 由
由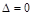 得
得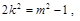 且
且 又
又
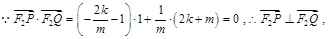 故结论成立. 13分
故结论成立. 13分
考点:1.椭圆的方程及其简单几何性质;2.直线与椭圆的位置关系;3.解析几何定点问题.

练习册系列答案
相关题目
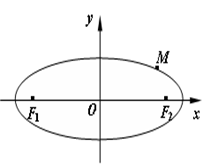
 中,已知椭圆
中,已知椭圆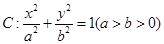 经过点
经过点
 ,椭圆的离心率
,椭圆的离心率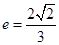 .
.
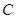 的方程;
的方程; 、
、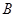 .若
.若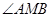 的平分线与
的平分线与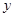 轴平行, 试探究直线
轴平行, 试探究直线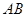 的斜率是否为定值?若是, 请给予证明;若不是, 请说明理由.
的斜率是否为定值?若是, 请给予证明;若不是, 请说明理由. 的最小值.
的最小值.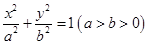 的离心率为
的离心率为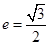 ,直线
,直线 与以原点为圆心、椭圆
与以原点为圆心、椭圆 的短半轴长为半径的圆
的短半轴长为半径的圆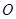 相切.
相切.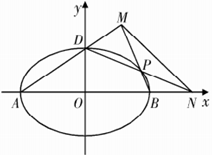
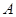 、
、 、
、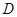 是椭圆
是椭圆 是椭圆
是椭圆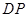 交
交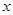 轴于点
轴于点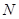 ,直线
,直线 交
交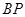 于点
于点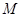 ,设
,设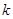 ,
,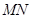 的斜率为
的斜率为 ,求证:
,求证: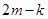 为定值.
为定值.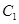 的参数方程为
的参数方程为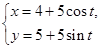 (
(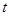 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线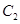 的极坐标方程为
的极坐标方程为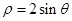 .
.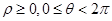 ).
). :
:
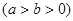 ,
,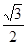 ,求椭圆的标准方程;
,求椭圆的标准方程;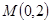 的直线
的直线 与椭圆
与椭圆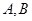 ,且
,且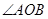 为锐角(
为锐角( 为坐标原点),求直线
为坐标原点),求直线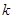 的取值范围;
的取值范围;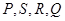 四点,设原点
四点,设原点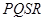 的一边距离为
的一边距离为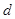 ,试求
,试求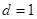 时
时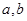 满足的条件.
满足的条件.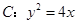 焦点为
焦点为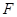 ,直线
,直线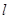 经过点
经过点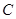 相交于
相交于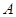 ,
,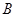 两点
两点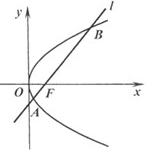
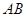 的中点在直线
的中点在直线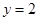 上,求直线
上,求直线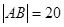 ,求直线
,求直线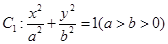 的离心率为
的离心率为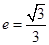 ,直线
,直线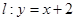 与以原点为圆心、以椭圆
与以原点为圆心、以椭圆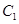 的短半轴长为半径的圆
的短半轴长为半径的圆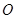 相切.
相切.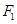 ,右焦点为
,右焦点为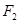 ,直线
,直线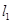 过点
过点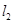 垂直于
垂直于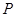 ,线段
,线段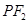 的垂直平分线交
的垂直平分线交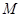 ,求点
,求点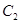 的方程;
的方程; 轴交于点
轴交于点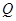 ,不同的两点
,不同的两点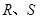 在
在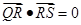 ,求
,求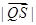 的取值范围.
的取值范围. 的左右焦点为F1,F2,离心率为
的左右焦点为F1,F2,离心率为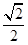 ,以线段F1 F2为直径的圆的面积为
,以线段F1 F2为直径的圆的面积为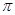 , (1)求椭圆的方程;(2) 设直线l过椭圆的右焦点F2(l不垂直坐标轴),且与椭圆交于A、B两点,线段AB的垂直平分线交x轴于点M(m,0),试求m的取值范围.
, (1)求椭圆的方程;(2) 设直线l过椭圆的右焦点F2(l不垂直坐标轴),且与椭圆交于A、B两点,线段AB的垂直平分线交x轴于点M(m,0),试求m的取值范围.