题目内容
已知集合M={x|y=-
}，集合N={y|y=ex，x∈R}（e是自然对数的底数），则M∩N=（ ）
| 1-x |
| A、{x|0＜x≤1} |
| B、{x|0＜x＜1} |
| C、{x|0＜x＜1} |
| D、∅ |
考点：交集及其运算
专题：集合
分析：求出M中x的范围确定出M，求出N中y的范围确定出N，找出M与N的交集即可．
解答：
解：由M中y=-
，得到1-x≥0，即x≤1，
∴M={x|0＜x≤1}，
由N中y=ex，x∈R，得到y＞0，即N={y|y＞0}，
则M∩N={x|0＜x≤1}，
故选：A．
| 1-x |
∴M={x|0＜x≤1}，
由N中y=ex，x∈R，得到y＞0，即N={y|y＞0}，
则M∩N={x|0＜x≤1}，
故选：A．
点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
相关题目
已知-9，a1，a2，-1四个实数成等差数列，-9，b1，b2，b3，-1五个实数成等比数列，则b2（a2-a1）的值等于（ ）
| A、-8 | ||
| B、8 | ||
C、-
| ||
D、
|
命题“?x0∈R，x＞1”否定是（ ）
| A、?x∈R，x＞1 |
| B、?x0∈R，x0≤1 |
| C、?x∈R，x≤1 |
| D、?x0∈R，x0＜1 |
在复平面内，复数Z=
+i3对应的点位于（ ）
| 2 |
| 3-i |
| A、第四象限 | B、第三象限 |
| C、第二象限 | D、第一象限 |
“sinθ=
”是“θ=
”的（ ）
| ||
| 2 |
| π |
| 3 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
在△ABC中，下列等式恒成立的是（ ）
| A、csinA=asinB |
| B、bcosA=acosB |
| C、asinA=bsinB |
| D、asinB=bsinA |
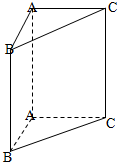如图，在直三棱柱ABC-A1B1C1中，AB=1，AC=AA1=