题目内容
12.已知a,b,c分别是△ABC内角A,B,C的对边,sin2B=2sinAsinC.(Ⅰ)若a=b,求cosB;
(Ⅱ)设B=90°,且a=$\sqrt{2}$,求△ABC的面积.
分析 (I)sin2B=2sinAsinC,由正弦定理可得:b2=2ac,再利用余弦定理即可得出.
(II)利用(I)及勾股定理可得c,再利用三角形面积计算公式即可得出.
解答 解:(I)∵sin2B=2sinAsinC,
由正弦定理可得:$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=\frac{1}{k}$>0,
代入可得(bk)2=2ak•ck,
∴b2=2ac,
∵a=b,∴a=2c,
由余弦定理可得:cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{{a}^{2}+\frac{1}{4}{a}^{2}-{a}^{2}}{2a×\frac{1}{2}a}$=$\frac{1}{4}$.
(II)由(I)可得:b2=2ac,
∵B=90°,且a=$\sqrt{2}$,
∴a2+c2=b2=2ac,解得a=c=$\sqrt{2}$.
∴S△ABC=$\frac{1}{2}ac$=1.
点评 本题考查了正弦定理余弦定理、勾股定理、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
2.某三棱锥的三视图如图所示,则该三棱锥的表面积是( )


| A. | 2+$\sqrt{5}$ | B. | 4+$\sqrt{5}$ | C. | 2+2$\sqrt{5}$ | D. | 5 |
3.已知A,B为双曲线E的左,右顶点,点M在E上,△ABM为等腰三角形,顶角为120°,则E的离心率为( )
| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
7.函数f(x)=cos(ωx+φ)的部分图象如图所示,则f(x)的单调递减区间为( )


| A. | (kπ-$\frac{1}{4}$,kπ+$\frac{3}{4}$,),k∈z | B. | (2kπ-$\frac{1}{4}$,2kπ+$\frac{3}{4}$),k∈z | ||
| C. | (k-$\frac{1}{4}$,k+$\frac{3}{4}$),k∈z | D. | ($2k-\frac{1}{4}$,2k+$\frac{3}{4}$),k∈z |
17.若空间中n个不同的点两两距离都相等,则正整数n的取值( )
| A. | 至多等于3 | B. | 至多等于4 | C. | 等于5 | D. | 大于5 |
4.设集合M={x|x2=x},N={x|lgx≤0},则M∪N=( )
| A. | [0,1] | B. | (0,1] | C. | [0,1) | D. | (-∞,1] |
1.设D为△ABC所在平面内一点,$\overrightarrow{BC}=3\overrightarrow{CD}$,则( )
| A. | $\overrightarrow{AD}=-\frac{1}{3}\overrightarrow{AB}+\frac{4}{3}\overrightarrow{AC}$ | B. | $\overrightarrow{AD}=\frac{1}{3}\overrightarrow{AB}-\frac{4}{3}\overrightarrow{AC}$ | C. | $\overrightarrow{AD}=\frac{4}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$ | D. | $\overrightarrow{AD}=\frac{4}{3}\overrightarrow{AB}-\frac{1}{3}\overrightarrow{AC}$ |
2.阅读如图的程序框图,运行相应的程序,则输出S的值为( )
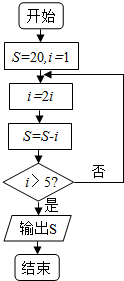

| A. | -10 | B. | 6 | C. | 14 | D. | 18 |