题目内容
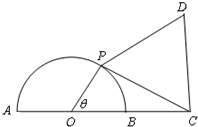 如图,已知⊙O的半径为1,点C在直径AB的延长线上,BC=1,点P是半圆上的一个动点,以PC为边作正三角形PCD,且点D与圆心分别在PC两侧.
如图,已知⊙O的半径为1,点C在直径AB的延长线上,BC=1,点P是半圆上的一个动点,以PC为边作正三角形PCD,且点D与圆心分别在PC两侧.(1)若∠POB=θ,试将四边形OPDC的面积y表示成θ的函数;
(2)求四边形OPDC面积的最大值?
分析:(1)先利用余弦定理求出PC的值,再将四边形OPDC的面积分解成两个三角形的面积的和,从而得到y关于θ的函数;
(2)由(1)知y=2sin(θ-
)+
,利用三角函数的值域可求最值.
(2)由(1)知y=2sin(θ-
| π |
| 3 |
5
| ||
| 4 |
解答:
,
∴当θ=
时,y max=2+
|
|
∴当θ=
| 5π |
| 6 |
5
| ||
| 4 |
点评:本题将三角函数与解三角形结合起来,关键是利用余弦定理求边,再求面积,三角函数求最值应注意角的范围.

练习册系列答案
相关题目
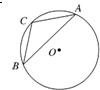
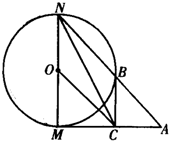 选修4-1:几何证明选讲
选修4-1:几何证明选讲