题目内容
如图,已知⊙O的半径为2,弦AB的长为2| 3 |
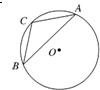
分析:首先做出辅助线,连接B、A与圆心再在优弧上找一点D,做出角ADB,根据直角三角形中三角函数的定义和特殊角的三角函数,写出锐角的值,根据同弧所对的圆周角和圆心角之间的关系,得到角D,根据圆内接四边形写出要求的结果.
解答:解:连接OA、OB,过O作OE⊥AB,E为垂足,则AE=BE.
在Rt△AOE中,OA=2,AE=
AB=
×2
=
,
∴sin∠AOE=
=
,
∴∠AOE=60°,
∴∠AOB=2∠AOE=120°,在优弧
上任取一点D(不与A、B重合),
∴∠ADB=
∠AOB=60°,
∴∠ACB=180°-∠ADB=120°.
在Rt△AOE中,OA=2,AE=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |

∴sin∠AOE=
| AE |
| OA |
| ||
| 2 |
∴∠AOE=60°,
∴∠AOB=2∠AOE=120°,在优弧
 |
| AB |
∴∠ADB=
| 1 |
| 2 |
∴∠ACB=180°-∠ADB=120°.
点评:本题考查圆内接四边形的性质,考查同弧所对的圆周角和圆心角之间的关系,考查直角三角形的性质,考查三角函数的定义,是一个比较简单的综合题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
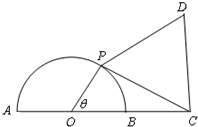 如图,已知⊙O的半径为1,点C在直径AB的延长线上,BC=1,点P是半圆上的一个动点,以PC为边作正三角形PCD,且点D与圆心分别在PC两侧.
如图,已知⊙O的半径为1,点C在直径AB的延长线上,BC=1,点P是半圆上的一个动点,以PC为边作正三角形PCD,且点D与圆心分别在PC两侧. 选修4-1:几何证明选讲
选修4-1:几何证明选讲