题目内容
 选修4-1:几何证明选讲
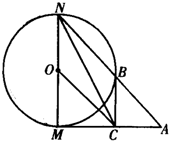
选修4-1:几何证明选讲如图,已知⊙O的半径为1,MN是⊙O的直径,过M点作⊙O的切线AM,C是AM的中点,AN交⊙O于B点,若四边形BCON是平行四边形;
(Ⅰ)求AM的长;
(Ⅱ)求sin∠ANC.
分析:(Ⅰ)连接BM,则平行四边形BCON中证出BC∥MN,由⊙O的切线AM⊥MN得到BC⊥AM,结合C是AM的中点得到△ABM中BM=BA.由MN是⊙O的直径,得∠MBN=90°,因此得到△NAM是等腰直角三角形,故AM=MN=2.
(II)作CE⊥AN于E点,等腰Rt△CEA中算出CE=
,Rt△MNC中算出CN=
,从而可得Rt△ENC中,sin∠ANC=
.
(II)作CE⊥AN于E点,等腰Rt△CEA中算出CE=
| ||
| 2 |
| 5 |
| ||
| 10 |
解答: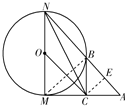 解:(Ⅰ)连接BM,则
解:(Ⅰ)连接BM,则
∵MN是⊙O的直径,∴∠MBN=90°,
∵四边形BCON是平行四边形,∴BC∥MN,
又∵AM是⊙O的切线,可得MN⊥AM,∴BC⊥AM,
∵C是AM的中点,∴BC是△ABM的中线,
由此可得△ABM是等腰三角形,即BM=BA,
∵∠MBN=90°,∴∠BMA=∠A=45°,
因此得到Rt△NAM是等腰直角三角形,故AM=MN=2.…(5分)
(Ⅱ)作CE⊥AN于E点,则
由(I),得△CEA是等腰直角三角形,且AC=1
∴CE=
AC=
,
∵Rt△MNC中,MN=2,MC=1,∴CN=
=
,
故Rt△ENC中,sin∠ANC=
=
.…(10分)
 解:(Ⅰ)连接BM,则
解:(Ⅰ)连接BM,则∵MN是⊙O的直径,∴∠MBN=90°,
∵四边形BCON是平行四边形,∴BC∥MN,
又∵AM是⊙O的切线,可得MN⊥AM,∴BC⊥AM,
∵C是AM的中点,∴BC是△ABM的中线,
由此可得△ABM是等腰三角形,即BM=BA,
∵∠MBN=90°,∴∠BMA=∠A=45°,
因此得到Rt△NAM是等腰直角三角形,故AM=MN=2.…(5分)
(Ⅱ)作CE⊥AN于E点,则
由(I),得△CEA是等腰直角三角形,且AC=1
∴CE=
| ||
| 2 |
| ||
| 2 |
∵Rt△MNC中,MN=2,MC=1,∴CN=
| 22+12 |
| 5 |
故Rt△ENC中,sin∠ANC=
| CE |
| NC |
| ||
| 10 |
点评:本题给出圆O的垂直于直径MN的一条切线AM,在已知△NAM是等腰直角三角形的情况下求线段的长,并求sin∠ANC的值.着重考查了圆的切线的性质、直径所对的圆周角和直角三角形中三角函数的定义等知识,属于中档题.

练习册系列答案
相关题目
 选修4-1:几何证明选讲
选修4-1:几何证明选讲 A、选修4-1:几何证明选讲
A、选修4-1:几何证明选讲  选修4-1:几何证明选讲
选修4-1:几何证明选讲 (2012•徐州模拟)选修4-1:几何证明选讲
(2012•徐州模拟)选修4-1:几何证明选讲 (2013•南京二模)选修4-1:几何证明选讲
(2013•南京二模)选修4-1:几何证明选讲