题目内容
7.已知函数f(x)=alnx+bx(a,b∈R),曲线y=f(x)在点(1,f(1))处的切线方程为x-2y-2=0.(Ⅰ)求f(x)的解析式;
(Ⅱ)当x>1时,f(x)+$\frac{k}{x}$<0恒成立,求实数k的取值范围.
分析 (Ⅰ)求导数得f′(x)=$\frac{a}{x}$+b,由导数几何意义得曲线y=f(x)在点(1,f(1))处的切线斜率为k=f′(1)=$\frac{1}{2}$,且f(1)=$\frac{1}{2}$,联立求得a=1,b=-$\frac{1}{2}$,从而确定f(x)的解析式;
(Ⅱ)由(Ⅰ)知,不等式等价于lnx-$\frac{x}{2}$+$\frac{k}{x}$<0,参变分离为k<$\frac{{x}^{2}}{2}$-xlnx,利用导数求右侧函数的最小值即可.
解答 解:(Ⅰ)∵f(x)=alnx+bx,∴f′(x)=$\frac{a}{x}$+b.
∵直线x-2y-2=0的斜率为$\frac{1}{2}$,且曲线y=f(x)过点(1,-$\frac{1}{2}$),
∴$\left\{\begin{array}{l}{f(1)=-\frac{1}{2}}\\{f′(1)=\frac{1}{2}}\end{array}\right.$即$\left\{\begin{array}{l}{b=-\frac{1}{2}}\\{a+b=\frac{1}{2}}\end{array}\right.$解得a=1,b=-$\frac{1}{2}$.
所以f(x)=lnx-$\frac{1}{2}$x;
(Ⅱ)由(Ⅰ)得当x>1时,f(x)+$\frac{k}{x}$<0恒成立即lnx-$\frac{x}{2}$+$\frac{k}{x}$<0,等价于k<$\frac{{x}^{2}}{2}$-xlnx.
令g(x)=$\frac{{x}^{2}}{2}$-xlnx,则g′(x)=x-1-lnx.
令h(x)=x-1-lnx,则h′(x)=1-$\frac{1}{x}$.
当x>1时,h′(x)>0,函数h(x)在(1,+∞)上单调递增,故h(x)>h(1)=0.
从而,当x>1时,g′(x)>0,即函数g(x)在(1,+∞)上单调递增,
故g(x)>g(1)=$\frac{1}{2}$.
因此,当x>1时,k<$\frac{{x}^{2}}{2}$-xlnx恒成立,则k≤$\frac{1}{2}$.
∴k的取值范围是(-∞,$\frac{1}{2}$].
点评 本题考查了导数的综合应用:求切线方程和求单调区间、极值和最值,及恒成立问题的应用,属于中档题.

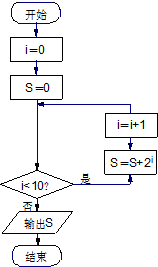
| A. | 1023 | B. | 1024 | C. | 511 | D. | 2047 |
 如图,在空间直角坐标系中有直三棱柱ABC-A1B1C1,CA=CC1=2CB,则直线BC1与直线AB1E夹角的余弦值为( )
如图,在空间直角坐标系中有直三棱柱ABC-A1B1C1,CA=CC1=2CB,则直线BC1与直线AB1E夹角的余弦值为( )| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{5}{2}$ |
| A. | $\frac{{2\sqrt{2}}}{5}$ | B. | $\frac{{3\sqrt{2}}}{5}$ | C. | $\frac{{4\sqrt{2}}}{5}$ | D. | $\sqrt{2}$ |
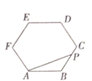 如图所示,点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动,其中AB=4,则$\overrightarrow{AP}$$•\overrightarrow{AB}$的取值区间为( )
如图所示,点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动,其中AB=4,则$\overrightarrow{AP}$$•\overrightarrow{AB}$的取值区间为( )| A. | [-2,6] | B. | [-8,24] | C. | [0,4] | D. | [4,6] |
| A. | A,C为对立事件 | B. | A,B为对立事件 | ||
| C. | A,C为互斥事件,但不是对立事件 | D. | A,B为互斥事件,但不是对立事件 |
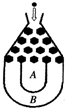 将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落的过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$,则小球落入A袋中的概率为$\frac{3}{4}$.
将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落的过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$,则小球落入A袋中的概率为$\frac{3}{4}$.