题目内容
在数列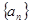 中,如果存在常数
中,如果存在常数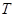
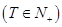 ,使得
,使得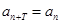 对于任意正整数
对于任意正整数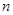 均成立,那么就称数列
均成立,那么就称数列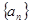 为周期数列,其中
为周期数列,其中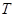 叫做数列
叫做数列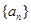 的周期. 已知数列
的周期. 已知数列 满足
满足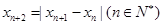 ,若
,若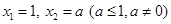 ,当数列
,当数列 的周期为
的周期为 时,则数列
时,则数列 的前2012项的和
的前2012项的和 为( )
为( )
| A.1339+a | B.1340+a | C.1341+a | D.1342+a |
D
解析试题分析:先要弄清题意中所说的周期数列的含义,然后利用这个定义,针对题目中的数列的周期,先求x3,再前三项和s3,最后求s2012.
∵xn+1=|xn-xn-1|(n≥2,n∈N*),且x1=1,x2=a(a≤1,a≠0),∴x3=|x2-x1|=1-a,∴该数列的前3项的和s3=1+a+(1-a)=2∵数列{xn}周期为3,∴该数列的前2012项的和s2012=s2010+x1+x2=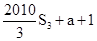 =1341+a,选B.
=1341+a,选B.
考点:本试题主要以周期数列为载体,考查数列具的周期性,考查该数列的前n项和.
点评:解决该试题的关键在于应由题意先求一个周期的和,再求该数列的前n项和sn.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
若数列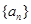 满足
满足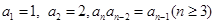 ,则
,则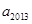 的值为 ( )
的值为 ( )
| A.2 | B. | C.1 | D. |
在各项都为正数的等比数列{an}中,首项a1=3,前三项和为21,则a3+ a4+ a5="(" )
| A.33 | B.72 | C.84 | D.189 |
实数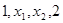 成等差数列,
成等差数列,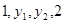 成等比数列,则
成等比数列,则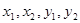 的大小关系是( )
的大小关系是( )
A.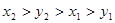 | B.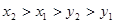 |
C.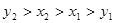 | D.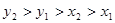 |
已知数列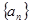 的前
的前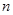 项和
项和 ,第
,第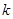 项满足
项满足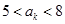 ,则
,则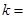
| A.9 | B.8 | C.7 | D.6 |
 元的一年定期储蓄,若年利率为
元的一年定期储蓄,若年利率为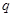 保持不变,且每年到期的存款本息自动转为新的一年定期,到2004年6月1日甲去银行不再存款,而是将所有存款的本息全部取回,则取回的金额是( )
保持不变,且每年到期的存款本息自动转为新的一年定期,到2004年6月1日甲去银行不再存款,而是将所有存款的本息全部取回,则取回的金额是( )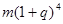 元
元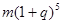 元
元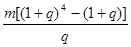 元
元 元
元 ,
,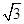 ,
,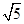 ,…,
,…,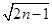 ,…,则
,…,则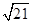 是这个数列的第 项.
是这个数列的第 项.