题目内容
实数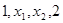 成等差数列,
成等差数列,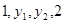 成等比数列,则
成等比数列,则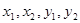 的大小关系是( )
的大小关系是( )
A.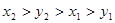 | B.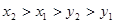 |
C.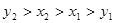 | D.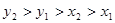 |
A
解析试题分析:根据等差数列的性质,由于实数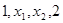 成等差数列,故有
成等差数列,故有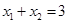 ,且等差数列的通项公式可知公差为d=
,且等差数列的通项公式可知公差为d=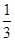 ,
,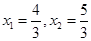 ,
,
又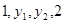 成等比数列,结合等比中项的性质可知,
成等比数列,结合等比中项的性质可知,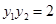 ,那么可知公比为
,那么可知公比为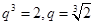 ,那么
,那么 ,通过平方作差可以比较大小得到为选项A.
,通过平方作差可以比较大小得到为选项A.
考点:本试题考查了等差数列的对等差中项的性质,以及等比数列的等比中项的性质的运用。
点评:解决该试题的关键是能利用已知中的数列的项求解出各个项的值,然后结合指数幂的运算来比较大小得到结论,属于基础题。

练习册系列答案
相关题目
已知数列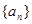 中,
中,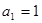 ,2
,2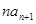 =
=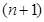
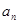 ,则数列
,则数列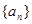 的通项公式为( )
的通项公式为( )
A.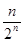 | B.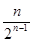 | C.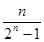 | D.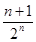 |
已知数列 成等差数列,
成等差数列,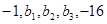 成等比数列,则
成等比数列,则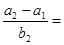 ( )
( )
A.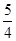 | B.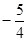 | C.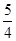 或 或 | D. |
已知数列 满足:
满足: ,
, ,当且仅当
,当且仅当 时
时 最小,则实数
最小,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C.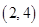 | D. |
数列 满足
满足 ,且对任意的
,且对任意的
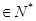 都有:
都有: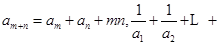
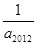 等于 ( )
等于 ( )
A. | B.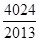 | C.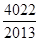 | D.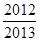 |
在数列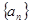 中,如果存在常数
中,如果存在常数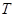
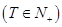 ,使得
,使得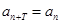 对于任意正整数
对于任意正整数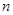 均成立,那么就称数列
均成立,那么就称数列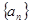 为周期数列,其中
为周期数列,其中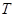 叫做数列
叫做数列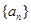 的周期. 已知数列
的周期. 已知数列 满足
满足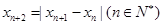 ,若
,若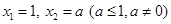 ,当数列
,当数列 的周期为
的周期为 时,则数列
时,则数列 的前2012项的和
的前2012项的和 为( )
为( )
| A.1339+a | B.1340+a | C.1341+a | D.1342+a |
已知数列{an}的通项公式为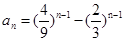 ,则数列{an}
,则数列{an}
| A.有最大项,没有最小项 | B.有最小项,没有最大项 |
| C.既有最大项又有最小项 | D.既没有最大项也没有最小项 |
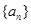 满足条件
满足条件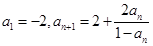 , 则
, 则 = ;
= ;