题目内容
已知数列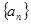 的前
的前 项和
项和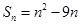 ,第
,第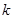 项满足
项满足 ,则
,则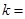
| A.9 | B.8 | C.7 | D.6 |
B
解析试题分析:因为an= ,那么可知= an=
,那么可知= an=
∵n=1时适合an=2n-10,∴an=2n-10.
∵5<ak<8,∴5<2k-10<8,
∴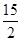 <k<9,又∵k∈N+,∴k=8,
<k<9,又∵k∈N+,∴k=8,
故选B.
考点:本题主要考查考查数列的通项公式的求法.
点评:解决该试题的关键是解题时要注意公式an= ,由第k项满足5<ak<8,求出k.
,由第k项满足5<ak<8,求出k.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
已知数列 ,
, ,若该数列是递减数列,则实数
,若该数列是递减数列,则实数 的取值范围是( )
的取值范围是( )
A.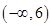 | B. | C. | D.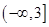 |
在8×8棋盘的64个方格中,共有由整数个小方格组成的大小或位置不同的正方形的个数为
| A.64 | B.128 | C.204 | D.408 |
在数列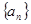 中,如果存在常数
中,如果存在常数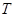
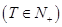 ,使得
,使得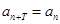 对于任意正整数
对于任意正整数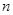 均成立,那么就称数列
均成立,那么就称数列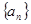 为周期数列,其中
为周期数列,其中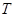 叫做数列
叫做数列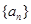 的周期. 已知数列
的周期. 已知数列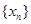 满足
满足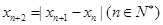 ,若
,若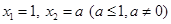 ,当数列
,当数列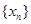 的周期为
的周期为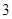 时,则数列
时,则数列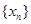 的前2012项的和
的前2012项的和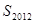 为( )
为( )
| A.1339+a | B.1340+a | C.1341+a | D.1342+a |
 的图象上存在不同的三点到原点的距离构成等比数列,则以下不可能成为该等比数列的公比的数是
的图象上存在不同的三点到原点的距离构成等比数列,则以下不可能成为该等比数列的公比的数是

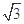

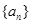 的首相
的首相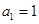 ,和递推关系
,和递推关系 (
(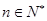 且
且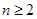 ),探求其通项公式为____________.
),探求其通项公式为____________.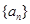 满足
满足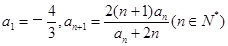 ,则
,则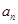 的最小值是
的最小值是  中,
中,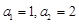 ,且
,且 ,则
,则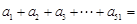 .
.