题目内容
在2000年至2003年期间,甲每年6月1日都到银行存入 元的一年定期储蓄,若年利率为
元的一年定期储蓄,若年利率为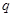 保持不变,且每年到期的存款本息自动转为新的一年定期,到2004年6月1日甲去银行不再存款,而是将所有存款的本息全部取回,则取回的金额是( )
保持不变,且每年到期的存款本息自动转为新的一年定期,到2004年6月1日甲去银行不再存款,而是将所有存款的本息全部取回,则取回的金额是( )
A.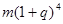 元 元 | B.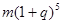 元 元 |
C.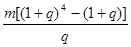 元 元 | D. 元 元 |
D
解析试题分析:2000年的m元到了2004年本息和为m(1+q)4,
2001年的m元到了2004年本息和为m(1+q)3,
2002年的m元到了2004年本息和为m(1+q)2,
2003年的m元到了2004年本息和为m(1+q),
∴所有金额为m(1+q)+m(1+q)2+m(1+q)3+m(1+q)4= ,
,
故选D.
考点:本题主要考查等比数列的应用,等比数列的通项公式、前n项和公式。
点评:典型题,综合应用等比数列的通项公式、前n项和公式,解决实际问题。该题有些陈旧,建议与时俱进,修改年份。

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
已知数列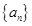 的前
的前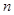 项和
项和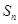 满足:
满足: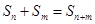 ,且
,且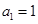 ,那么
,那么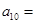 ( )
( )
| A.1 | B.9 | C.10 | D.55 |
若数列 满足
满足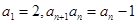 ,则
,则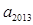 的值为
的值为
A.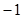 | B.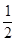 | C.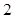 | D.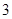 |
已知数列 满足
满足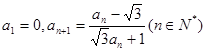 ,则
,则 等于( )
等于( )
A.0 | B.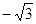 | C.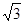 | D. |
已知数列 成等差数列,
成等差数列,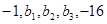 成等比数列,则
成等比数列,则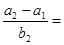 ( )
( )
A.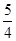 | B.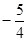 | C.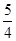 或 或 | D. |
在8×8棋盘的64个方格中,共有由整数个小方格组成的大小或位置不同的正方形的个数为
| A.64 | B.128 | C.204 | D.408 |
已知数列 满足:
满足: ,
, ,当且仅当
,当且仅当 时
时 最小,则实数
最小,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C.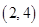 | D. |
在数列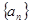 中,如果存在常数
中,如果存在常数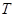
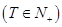 ,使得
,使得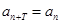 对于任意正整数
对于任意正整数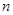 均成立,那么就称数列
均成立,那么就称数列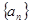 为周期数列,其中
为周期数列,其中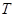 叫做数列
叫做数列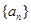 的周期. 已知数列
的周期. 已知数列 满足
满足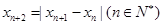 ,若
,若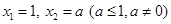 ,当数列
,当数列 的周期为
的周期为 时,则数列
时,则数列 的前2012项的和
的前2012项的和 为( )
为( )
| A.1339+a | B.1340+a | C.1341+a | D.1342+a |