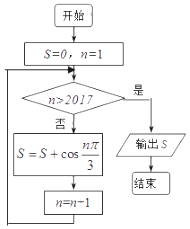
题目内容
【题目】已知PC⊥平面ABC,AC=2 ![]() ,PC=BC,AB=4,∠BAC=30°. 点D是线段AB上靠近B的四等分点,PE∥CB,PC∥EB.
,PC=BC,AB=4,∠BAC=30°. 点D是线段AB上靠近B的四等分点,PE∥CB,PC∥EB.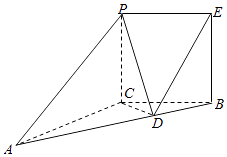
(Ⅰ)证明:直线AB⊥平面PCD;
(Ⅱ)若F为线段AC上靠近C的四等分点,求平面PDF与平面CBD所成锐二面角的正切值.
【答案】解:(Ⅰ)证明:在△ABC中,由余弦定理可得BC2=AC2+AB2﹣2ACABcos30°= ![]() ,
,
所以BC=2,AC2+BC2=AB2,所以AC⊥BC,∠ABC=60°,又 ![]() ,
,
在△BCD中,由余弦定理,得: ![]() ,
,
∴ ![]() ,∵BD2+CD2=BC2,∴BD⊥CD;即CD⊥AB
,∵BD2+CD2=BC2,∴BD⊥CD;即CD⊥AB
∵PC⊥平面ABC,AB平面ABC,所以AB⊥PC;
又PC∩CD=C,PC,CD平面PCD,所以AB⊥平面PCD.…
(Ⅱ)因为PC⊥平面ABC,BC平面ABC,所以PC⊥BC,又因为AC⊥BC,PC∩AC=C,所以BC⊥平面PAC.
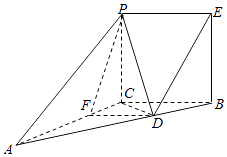
因为 ![]() ,所以DF∥BC,所以DF⊥平面PAC,所以DF⊥FC,DF⊥PF,所以∠PFC就是平面PDF与平面CBD所成二面角的平面角,
,所以DF∥BC,所以DF⊥平面PAC,所以DF⊥FC,DF⊥PF,所以∠PFC就是平面PDF与平面CBD所成二面角的平面角, ![]() 即平面PDF与平面CBD所成锐二面角的正切值为
即平面PDF与平面CBD所成锐二面角的正切值为 ![]() …
…
【解析】(1)在△ABC中,根据余弦定理求出BC=2,由勾股定理可得出AC⊥BC,在△BCD中,由余弦定理求出CD=![]() ,再根据勾股定理可得BD⊥CD,即CD⊥AB,又根据PC⊥平面ABC,得到AB⊥PC,不难证出结果,(2)根据题意不难证明出∠PFC就是平面PDF与平面CBD所成二面角的平面角,通过解三角形可得其正切值.
,再根据勾股定理可得BD⊥CD,即CD⊥AB,又根据PC⊥平面ABC,得到AB⊥PC,不难证出结果,(2)根据题意不难证明出∠PFC就是平面PDF与平面CBD所成二面角的平面角,通过解三角形可得其正切值.

练习册系列答案
相关题目