题目内容

10．设an=logn+1（n+2）（n∈N*），观察下列运算：a1•a2=log23•log34=$\frac{lg3}{lg2}•\frac{lg4}{lg3}$=2；a1•a2•a3•a4•a5•a6=log23•log34…log67•log78=$\frac{lg3}{lg2}•\frac{lg4}{lg3}…\frac{lg7}{lg6}•\frac{lg8}{lg7}$=3；则当a1•a2…ak=2015时，正整数k为（　　）
A．22015-2B．22015C．22015+2D．22015-4

分析 由题意知a1•a2•…•ak=$\frac{lg3}{lg2}$•$\frac{lg4}{lg3}$•$\frac{lg5}{lg4}$••$\frac{lg（k+2）}{lg（k+1）}$=2015，解方程即可得到结论．

解答 解：a1•a2••ak=$\frac{lg3}{lg2}$•$\frac{lg4}{lg3}$•$\frac{lg5}{lg4}$••$\frac{lg（k+2）}{lg（k+1）}$=$\frac{lg（k+2）}{lg2}$=log2（k+2），
由当a1•a2…ak=2015，
即log2（k+2）=2015，
解得k+2=22015，
即k=22015-2．
故选：A

点评 本题主要考查对数的基本运算，利用对数的换底公式将条件进行化简是解决本题的关键．解题时要注意公式的灵活运用．

练习册系列答案
相关题目
20．若z=$\frac{2-i}{2+i}$（i为虚数单位），则共轭复数$\overline z$在复平面内对应的点在第一象限．
1．若函数f（x）=log4（4x+1）+kx（x∈R）是偶函数．
（1）求实数k的值；
（2）若关于x的方程f（x）-m=0在[0，1]有解，求实数m的取值范围．
18．观察下列的规律：$\frac{1}{1}，\frac{1}{2}，\frac{2}{1}$，$\frac{1}{3}，\frac{2}{2}，\frac{3}{1}$，$\frac{1}{4}，\frac{2}{3}，\frac{3}{2}，\frac{4}{1}$…则第93个是（　　）
A．$\frac{1}{8}$B．$\frac{2}{13}$C．$\frac{8}{7}$D．$\frac{1}{14}$
5．在△ABC中，a，b，c分别为角A，B，C的对边，cos2$\frac{A}{2}$=$\frac{1}{2}$+$\frac{b}{2c}$，则△ABC的形状为直角三角形．
15．设等差数列{an}，{bn}的前n项和分别为Sn，Tn，若$\frac{a_n}{b_n}=\frac{2n-1}{n+1}$，则$\frac{{{S_{11}}}}{{{T_{11}}}}$=（　　）
A．$\frac{7}{4}$B．$\frac{11}{7}$C．2D．$\frac{7}{2}$
2．函数y=$\left\{\begin{array}{l}{3^x}，x∈（-∞，1]\\ 3-\frac{3}{x}，x∈（1，+∞）\end{array}$的值域为（　　）
A．（0，3）B．（0，3]C．（0，+∞）D．[0，+∞）
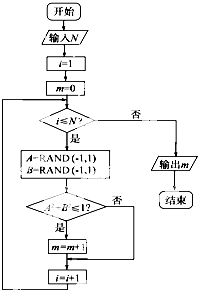19．如图所示的程序框图可用来估计π的值（假设函数RAND（-1，1）是产
生随机数的函数，它能随机产生区间（-1，1）内的任何一个实数）．
如果输入1000，输出的结果为788，则运用此方法估计的π的近似值为3.152．
20．已知定义在区间$[\;-π\;，\;\frac{2}{3}π\;]$上的函数y=f（x）的图象关于直线x=-$\frac{π}{6}$对称，当$x∈[\;-\frac{π}{6}\;，\;\frac{2}{3}π\;]$时，函数f（x）=Asin（ωx+ϕ）$（A＞0\;，\;ω＞0\;，\;-\frac{π}{2}＜ϕ＜\frac{π}{2}）$，其图象如图．
（1）求函数y=f（x）在$[\;-π\;，\;\frac{2}{3}π\;]$的表达式；
（2）求方程f（x）=$\frac{{\sqrt{2}}}{2}$的解．
（3）写出不等式f（x）＞$\frac{1}{2}$的解集（不需要过程）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网