题目内容
【题目】在四棱锥P﹣ABCD中,底面ABCD是菱形,PA⊥底面ABCD,M是棱PC上一点.若PA=AC=a,则当△MBD的面积为最小值时,直线AC与平面MBD所成的角为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:连结AC,BD交于O,在四棱锥P﹣ABCD中,底面ABCD是菱形,PA⊥底面ABCD,所以:PA⊥BD
AC⊥BD.
所以BD⊥平面PAC
进一步求出:BM=DM
过O点作OM⊥PC于M,
当△MBD的面积为最小时,只需OM最小即可.
若PA=AC=a
所以:∠ACP= ![]()
即为所求.
故选:B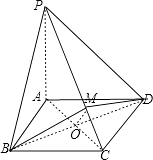
【考点精析】本题主要考查了空间角的异面直线所成的角的相关知识点,需要掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则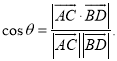 才能正确解答此题.
才能正确解答此题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目