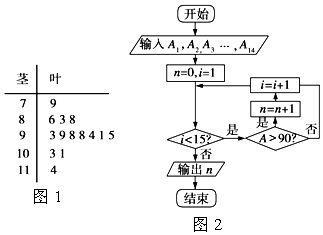
题目内容
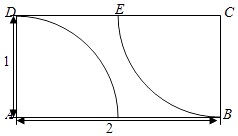
【题目】矩形区域 ABCD 中,AB 长为 2 千米,BC 长为 1 千米,在 A 点和 C 点处各有一个通信基站,其覆盖范围均为方圆 1 千米,若在该矩形区域内随意选取一地点,则该地点无信号的概率为 .
【答案】1﹣ ![]()
【解析】解:∵如图,扇形ADE的半径为1,圆心角等于90°,
∴扇形ADE的面积为S1= ![]() ×π×12=
×π×12= ![]() ,
,
同理可得,扇形CBF的在,面积S2= ![]() ,
,
又∵长方形ABCD的面积S=2×1=2,
∴在该矩形区域内随机地选一地点,则该地点无信号的概率是P= ![]() =1﹣
=1﹣ ![]() ,
,
所以答案是:1﹣ ![]() .
.
【考点精析】解答此题的关键在于理解几何概型的相关知识,掌握几何概型的特点:1)试验中所有可能出现的结果(基本事件)有无限多个;2)每个基本事件出现的可能性相等.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目