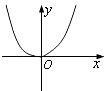题目内容
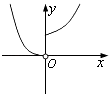
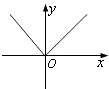
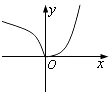
【题目】已知函数f(x)= ![]() 其中M∪P=R,则下列结论中一定正确的是( )
其中M∪P=R,则下列结论中一定正确的是( )
A.函数f(x)一定存在最大值
B.函数f(x)一定存在最小值
C.函数f(x)一定不存在最大值
D.函数f(x)一定不存在最小值
【答案】C
【解析】解:由函数y=2x的值域为(0,+∞),
y=x2的值域为[0,+∞),
且M∪P=R,
若M=(0,+∞),P=(﹣∞,0],
则f(x)的最小值为0,故D错;
若M=(﹣∞,2),P=[2,+∞),
则f(x)无最小值为,故B错;
由M∪P=R,可得图象无限上升,
则f(x)无最大值.
故选:C.
【考点精析】认真审题,首先需要了解函数的最值及其几何意义(利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值).

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目