题目内容
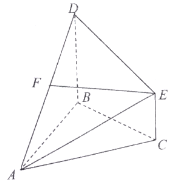
【题目】如图,已知![]() 为等边三角形,
为等边三角形,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,平面
,平面![]() 平面ABD,点E与点D在平面ABC的同侧,且
平面ABD,点E与点D在平面ABC的同侧,且![]() ,
,![]() .点F为AD中点,连接EF.
.点F为AD中点,连接EF.
(1)求证:![]() 平面ABC;
平面ABC;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)取AB中点为O,连接OC、OF,证明四边形OCEF为平行四边形,EF∥OC,然后证明EF∥平面ABC;
(2)以O为坐标原点,分别以![]() 、
、![]() 、
、![]() 的方向为x、y、z轴正方向,建立空间直角坐标系.不妨令正三角形ABC的边长为2,求出相关的的坐标,求出平面AEC的法向量,平面AED的法向量,取法向量的方向一进一出,利用空间向量的公式求解即可.
的方向为x、y、z轴正方向,建立空间直角坐标系.不妨令正三角形ABC的边长为2,求出相关的的坐标,求出平面AEC的法向量,平面AED的法向量,取法向量的方向一进一出,利用空间向量的公式求解即可.
(1)证明:取AB中点为O,连接OC、OF,∵O、F分别为AB、AD中点,
∴OF∥BD且BD=2OF,又CE∥BD且BD=2CE,∴CE∥OF且CE=OF,∴四边形OCEF为平行四边形,∴EF∥OC,
又OC平面ABC且EF平面ABC,∴EF∥平面ABC.
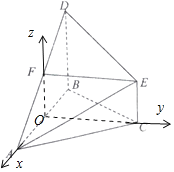
(2)∵三角形ABC为等边三角形,O为AB中点,∴OC⊥AB,∵平面ABC⊥平面ABD且平面ABC∩平面ABD=AB,
又BD⊥AB且BD平面ABD,∴BD⊥平面ABC,又OF∥BD,∴OF⊥平面ABC,
以O为坐标原点,分别以![]() 、
、![]() 、
、![]() 的方向为x、y、z轴正方向,建立空间直角坐标系.
的方向为x、y、z轴正方向,建立空间直角坐标系.
不妨令正三角形ABC的边长为2,则O(0,0,0),A(1,0,0),![]() ,
,![]() ,D(﹣1,0,2),
,D(﹣1,0,2),
∴![]() ,
,![]() ,
,![]() 设平面AEC的法向量为
设平面AEC的法向量为![]() ,则
,则 ,
,
不妨令![]() ,则
,则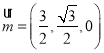 ,
,
设平面AED的法向量为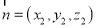 ,
,
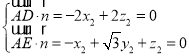 令
令![]()
得![]() ,
,
∴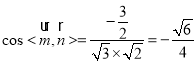 ,
,
∴所求二面角C﹣AE﹣D的余弦值为![]() .
.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目