题目内容
(本题满分14分)
已知两个命题r(x):sinx+cosx>m;s(x):x2+mx+1>0.如果对于任意实数x,r(x)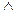 s(x) 为假,r(x)
s(x) 为假,r(x)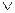 s(x)为真,求实数m的取值范围。
s(x)为真,求实数m的取值范围。
已知两个命题r(x):sinx+cosx>m;s(x):x2+mx+1>0.如果对于任意实数x,r(x)
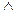 s(x) 为假,r(x)
s(x) 为假,r(x)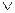 s(x)为真,求实数m的取值范围。
s(x)为真,求实数m的取值范围。.解:∵sinx+cosx=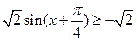
∴当r(x)为真命题时,m<-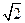 ……………… 3分
……………… 3分
又 若s(x)为真命题,则x2+mx+1>0恒成立,有△="m2-4<0,-2<m<2 " ……………… 6分
则由题知r(x)真,s(x)假时有m≤-2 ……………… 9分
r(x)假,s(x)真时有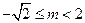 ……………… 12分
……………… 12分
故m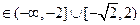 ……………… 14分
……………… 14分
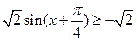
∴当r(x)为真命题时,m<-
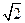 ……………… 3分
……………… 3分又 若s(x)为真命题,则x2+mx+1>0恒成立,有△="m2-4<0,-2<m<2 " ……………… 6分
则由题知r(x)真,s(x)假时有m≤-2 ……………… 9分
r(x)假,s(x)真时有
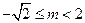 ……………… 12分
……………… 12分故m
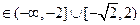 ……………… 14分
……………… 14分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
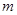 、
、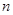 与平面
与平面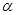 、
、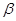 ,有下列四个命题:
,有下列四个命题: 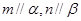 且
且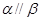 ,则
,则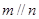 ;
; 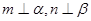 且
且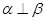 ,则
,则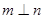 ;
;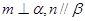 且
且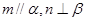 且
且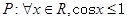 ,则( )
,则( )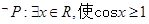
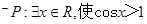
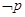 ”与命题“
”与命题“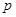 或
或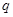 ”都是真命题,那么命题
”都是真命题,那么命题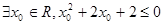 ,则
,则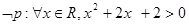
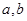 都是偶数,则
都是偶数,则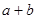 是偶数”否命题“若
是偶数”否命题“若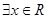 ,使
,使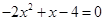 ”是假命题
”是假命题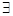 X∈R,lgX=0 B
X∈R,lgX=0 B 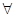 X∈R,X3﹥0 D
X∈R,X3﹥0 D 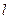 ,
,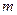 是两条不同的直线,
是两条不同的直线,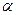 是一个平面,下列命题正确的是
是一个平面,下列命题正确的是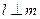 ,
,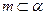 ,则
,则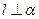
 ,则
,则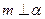
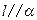 ,
, ,则
,则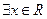 ,使
,使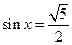 ;命题q:
;命题q: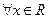 ,都有
,都有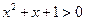 ,给出下列结论:①命题“p∧q”是真命题;②命题“p∧
,给出下列结论:①命题“p∧q”是真命题;②命题“p∧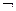 q”是假命题;③命题“p∨q”是真命题;④命题“
q”是假命题;③命题“p∨q”是真命题;④命题“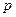 且
且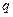 ”为假命题,则
”为假命题,则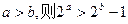 ”的否命题为“若
”的否命题为“若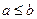 ,则
,则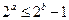 ”;
”;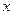 ∈R,
∈R,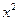 +1≥1”的否定是 “
+1≥1”的否定是 “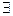
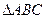 中,“
中,“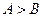 ”是“
”是“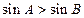 ”的充要条件.
”的充要条件.