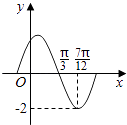题目内容
【题目】设直线l:y=k(x+1)(k≠0)与椭圆3x2+y2=a2(a>0)相交于A、B两个不同的点,与x轴相交于点C,记O为坐标原点. (Ⅰ)证明:a2> ![]() ;
;
(Ⅱ)若 ![]() ,求△OAB的面积取得最大值时的椭圆方程.
,求△OAB的面积取得最大值时的椭圆方程.
【答案】证明:(Ⅰ)由y=k(x+1)(k≠0)得 ![]() . 并代入椭圆方程3x2+y2=a2消去x得(3+k2)y2﹣6ky+3k2﹣k2a2=0 ①
. 并代入椭圆方程3x2+y2=a2消去x得(3+k2)y2﹣6ky+3k2﹣k2a2=0 ①
∵直线l与椭圆相交于两个不同的点得△=36k2﹣4(3+k2)(3k2﹣k2a2)>0,
∴ ![]() .
.
(Ⅱ)解:设A(x1 , y1),B(x2 , y2).
由①,得 ![]() ,②
,②
∵ ![]() ,而点C(﹣1,0),
,而点C(﹣1,0),
∴(﹣1﹣x1 , ﹣y1)=2(x2+1,y2),
得y1=﹣2y2代入②,得 ![]() ,③
,③
∴△OAB的面积 ![]() =
= ![]() =
= ![]() ≤
≤ ![]() =
= ![]() ,当且仅当k2=3,即
,当且仅当k2=3,即 ![]() 时取等号.
时取等号.
把k的值代入③可得 ![]() ,
,
将 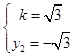 及
及 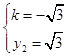 这两组值分别代入①,均可解出a2=15.
这两组值分别代入①,均可解出a2=15.
∴△OAB的面积取得最大值的椭圆方程是3x2+y2=15
【解析】(1)把直线l的方程代入椭圆方程,由直线与椭圆相交于A、B两个不同的点可得△>0,解出即可证明;(2)设A(x1 , y1),B(x2 , y2).利用根与系数的关系及向量相等得到y1 , y2的关系及可用k来表示,再利用三角形的面积公式∴△OAB的面积 ![]() 及基本不等式的性质即可得出取得面积最大值时的k的值,进而得到a的值.
及基本不等式的性质即可得出取得面积最大值时的k的值,进而得到a的值.
【考点精析】关于本题考查的椭圆的标准方程,需要了解椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 才能得出正确答案.
才能得出正确答案.

【题目】随着生活水平的提高,人们对空气质量的要求越来越高,某机构为了解公众对“车辆限行”的态度,随机抽查![]() 人,并将调查情况进行整理后制成下表:
人,并将调查情况进行整理后制成下表:
年龄(岁) |
|
|
|
|
|
频数 |
|
|
|
|
|
赞成人数 |
|
|
|
|
|
(1)世界联合国卫生组织规定: ![]() 岁为青年,
岁为青年, ![]() 为中年,根据以上统计数据填写以下
为中年,根据以上统计数据填写以下![]() 列联表:
列联表:
青年人 | 中年人 | 合计 | |
不赞成 | |||
赞成 | |||
合计 |
(2)判断能否在犯错误的概率不超过![]() 的前提下,认为赞成“车柄限行”与年龄有关?
的前提下,认为赞成“车柄限行”与年龄有关?
附: 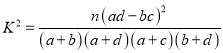 ,其中
,其中![]()
独立检验临界值表:
|
|
|
|
|
|
|
|
|
|
(3)若从年龄![]() 的被调查中各随机选取
的被调查中各随机选取![]() 人进行调查,设选中的两人中持不赞成“车辆限行”态度的人员为
人进行调查,设选中的两人中持不赞成“车辆限行”态度的人员为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.