Question

【题目】已知命题 p: 方程 在 上有且仅有一解；命题 q ：只有一个实数x满足不等式 .若命题“ p 或q ”是假命题，求a的取值范围．

Answer 1

【答案】【解答】由 ，得 .显然 所以 或.
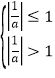
因为方程 a2x2+ax-2=0在[-1,1] 上有且仅有一解,故 ，或 ，所以.-2<a<-1或
因为只有一个实数x满足不等式x2+2ax+2a0 ，
所以V=4a2-8a=0 ,解得.a=0或a=2
因为命题“ p 或 q ”是假命题，所以命题 p 和 q 都是假命题,
所以 a 的取值范围是 {a|或-1≤a<0或0<a<1或a>2} 。
【解析】先求命题p和命题q的a的取值范围，再由判断复合命题的口诀（或命题：有真则真；且命题：有假则假；非命题：真假相反。）进行判断即可。