题目内容
数列{an}中，a1=1，对于所有的n≥2，n∈N*都有a1•a2•a3•…•an=n2，则a3+a4等于________．
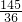
分析：由题设知a1•a2•a3•a4=16，a1•a2•a3=9，a1•a2=4，由此能得到a3+a4的结果．
解答：∵a1=1，对于所有的n≥2，n∈N*都有a1•a2•a3•…•an=n2，
∴a1•a2•a3•a4=16，a1•a2•a3=9，a1•a2=4，
∴a4=
，a3=
．∴a3+a4=
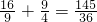．故答案为：
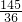．点评：本题考查数列的性质和应用，解题时要注意递推公式的灵活运用，由题设先求出a1•a2•a3•a4=16，a1•a2•a3=9，a1•a2=4，所以a4=
，a3=，由此能得到a3+a4的结果． 
练习册系列答案
相关题目
数列{an}中，a1=
，an+an+1=
，n∈N*，则
（a1+a2+…+an）等于（ ）
| 1 |
| 5 |
| 6 |
| 5n+1 |
| lim |
| n→∞ |
A、
| ||
B、
| ||
C、
| ||
D、
|