题目内容
【题目】椭圆
的右顶点和上顶点分别为
,斜率为
的直线
与椭圆
交于
两点(点
在第一象限).
(Ⅰ)求证：直线
的斜率之和为定值；
(Ⅱ)求四边形
面积的取值范围.
【答案】(Ⅰ)见解析；(Ⅱ)
.
【解析】
(Ⅰ)设直线
方程为：
代入
并整理得：
,利用韦达定理与斜率公式可得而
，化简即可得结果；(Ⅱ)设
的左顶点和下顶点分别为
、
,则直线、
、
为互相平行的直线,所以
、
两点到直线的距离等于两平行线、间的距离
.，利用弦长公式以及三角形面积公式可得
，从而可得结果.
(Ⅰ)设直线方程为：代入椭圆并整理得：
设
,则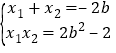
.
从而
所以直线
、
的斜率之和为定值0.
(Ⅱ)设的左顶点和下顶点分别为、,则直线、、为互相平行的直线,所以、两点到直线的距离等于两平行线、间的距离.
,又
点在第一象限,
.
【题目】2022年北京冬奥会的申办成功与“3亿人上冰雪”口号的提出，将冰雪这个冷项目迅速炒“热”．北京某综合大学计划在一年级开设冰球课程，为了解学生对冰球运动的兴趣，随机从该校一年级学生中抽取了100人进行调查，其中女生中对冰球运动有兴趣的占
，而男生有10人表示对冰球运动没有兴趣额．
（1）完成
列联表，并回答能否有
的把握认为“对冰球是否有兴趣与性别有关”？
有兴趣 | 没兴趣 | 合计 | |
男 | 55 | ||
女 | |||
合计 |
（2）已知在被调查的女生中有5名数学系的学生，其中3名对冰球有兴趣，现在从这5名学生中随机抽取3人，求至少有2人对冰球有兴趣的概率．
附表：
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【题目】某糕点房推出一类新品蛋糕，该蛋糕的成本价为4元，售价为8元．受保质期的影响，当天没有销售完的部分只能销毁．经过长期的调研，统计了一下该新品的日需求量．现将近期一个月（30天）的需求量展示如下：
日需求量x（个） | 20 | 30 | 40 | 50 |
天数 | 5 | 10 | 10 | 5 |
（1）从这30天中任取两天，求两天的日需求量均为40个的概率．
（2）以上表中的频率作为概率，列出日需求量
的分布列，并求该月的日需求量的期望．
（3）根据（2）中的分布列求得当该糕点房一天制作35个该类蛋糕时，对应的利润的期望值为
；现有员工建议扩大生产一天45个，求利用利润的期望值判断此建议该不该被采纳．