题目内容
设不等式2(log x)2+9(log
x)2+9(log x)+9≤0的解集为M,求当x∈M时函数f(x)=(log2
x)+9≤0的解集为M,求当x∈M时函数f(x)=(log2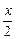 )(log2
)(log2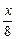 )的最大、最小值.
)的最大、最小值.
 x)2+9(log
x)2+9(log x)+9≤0的解集为M,求当x∈M时函数f(x)=(log2
x)+9≤0的解集为M,求当x∈M时函数f(x)=(log2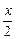 )(log2
)(log2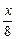 )的最大、最小值.
)的最大、最小值. ∴当log2x=2,即x=4时ymin=-1;当log2x=3,即x=8时,ymax=0.
∵2(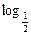 x)2+9(
x)2+9(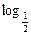 x)+9≤0
x)+9≤0
∴(2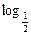 x+3)(
x+3)(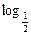 x+3)≤0. ∴-3≤
x+3)≤0. ∴-3≤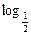 x≤-
x≤- .
.
即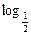 (
(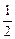 )-3≤
)-3≤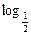 x≤
x≤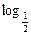 (
(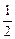 )
)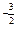
∴(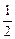 )
)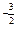 ≤x≤(
≤x≤(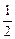 )-3,∴2
)-3,∴2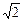 ≤x≤8
≤x≤8
即M={x|x∈[2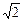 ,8]}
,8]}
又f(x)=(log2x-1)(log2x-3)=log22x-4log2x+3=(log2x-2)2-1.
∵2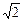 ≤x≤8,∴
≤x≤8,∴ ≤log2x≤3
≤log2x≤3
∴当log2x=2,即x=4时ymin=-1;当log2x=3,即x=8时,ymax="0. "
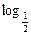 x)2+9(
x)2+9(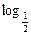 x)+9≤0
x)+9≤0∴(2
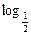 x+3)(
x+3)(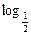 x+3)≤0. ∴-3≤
x+3)≤0. ∴-3≤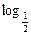 x≤-
x≤- .
. 即
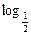 (
(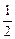 )-3≤
)-3≤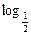 x≤
x≤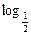 (
(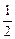 )
)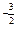
∴(
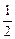 )
)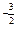 ≤x≤(
≤x≤(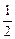 )-3,∴2
)-3,∴2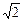 ≤x≤8
≤x≤8即M={x|x∈[2
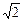 ,8]}
,8]}又f(x)=(log2x-1)(log2x-3)=log22x-4log2x+3=(log2x-2)2-1.
∵2
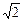 ≤x≤8,∴
≤x≤8,∴ ≤log2x≤3
≤log2x≤3∴当log2x=2,即x=4时ymin=-1;当log2x=3,即x=8时,ymax="0. "

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
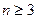 ,实数
,实数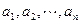 满足
满足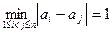 .求
.求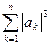 的最小值.
的最小值.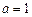 时,求所有使
时,求所有使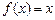 成立的
成立的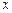 的值;
的值;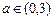 时,求函数
时,求函数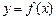 在闭区间
在闭区间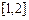 上的最小值;
上的最小值;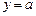 的交点个数
的交点个数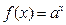 (
(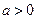 ,
,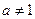 )在
)在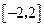 上函数值总小于
上函数值总小于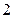 ,求实数
,求实数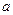 的取值范围.
的取值范围.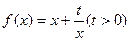 和点
和点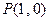 ,过点
,过点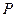 作曲线
作曲线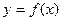 的两条切线
的两条切线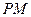 、
、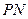 ,切点分别为
,切点分别为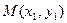 、
、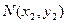 .
.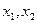 为关于
为关于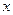 的方程
的方程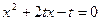 的两根;
的两根;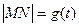 ,求函数
,求函数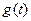 的表达式;
的表达式;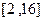 内总存在
内总存在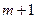 个实数
个实数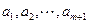 (可以相同),使得不等,则m的最大值,
(可以相同),使得不等,则m的最大值,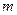 为正整数
为正整数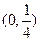 上为减函数的是( )
上为减函数的是( )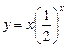 ;
;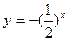 ;
;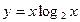 ;
;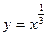
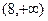 上为减函数,且函数y=f(x+8)函数为偶函数,
上为减函数,且函数y=f(x+8)函数为偶函数, ,若
,若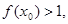 则
则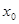 的取值范围是 。
的取值范围是 。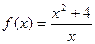 ,
, 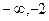 )上的单调性,并用定义加以证明。
)上的单调性,并用定义加以证明。