题目内容
(本小题满分12分)
如图所示的几何体中,四边形ABCD是等腰梯形,AD//CD,  ,FC
,FC  平面ABCD, AE
平面ABCD, AE  BD,CB =CD=-CF.
BD,CB =CD=-CF.
(Ⅰ)求证:平面ABCD  平面AED;
平面AED;
(Ⅱ)直线AF与面BDF所成角的余弦值
(Ⅰ)见解析 (Ⅱ)
解析试题分析:(Ⅰ)通过计算可证得AD⊥BD,又因为AE⊥BD,由线面垂直的判定定理得,BD⊥面ADE,由面面垂直的判定定理得,面ADE⊥面ABCD; (Ⅱ)由(Ⅰ)知AD⊥BD,同理可证AC⊥BC,因为CF⊥面ABCD,所以以CA,CB,CF分别为 建立空间直角坐标系,设BC=1,求出A、B、D,F点的坐标,求出
建立空间直角坐标系,设BC=1,求出A、B、D,F点的坐标,求出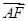 的坐标和平面BDF法向量的坐标,利用空间向量夹角公式计算出这两个向量夹角的余弦值,利用同脚三角函数基本关系求出向量夹角的正弦值即为线面夹角的余弦值.
的坐标和平面BDF法向量的坐标,利用空间向量夹角公式计算出这两个向量夹角的余弦值,利用同脚三角函数基本关系求出向量夹角的正弦值即为线面夹角的余弦值.
试题解析:(Ⅰ)∵四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,
∴∠ADC=∠BCD=120°,
又CB=CD,∴∠CDB=30°,∴∠ADB=90°,AD⊥BD,
又AE⊥BD,且AE∩AD=A,AE,AD?平面AED,
∴BD⊥平面AED,∴平面ABCD⊥平面AED.
(Ⅱ)连结AC,由(Ⅰ)知AD⊥BD,∴AC⊥BC,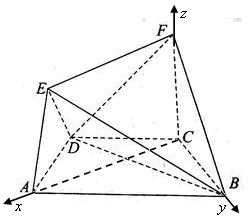
又FC⊥平面ABCD,∴CA,CB,CF两两垂直,
以C为坐标原点,建立空间直角坐标系,设CB=1,
则A( ,0,0),B(0,1,0),D(
,0,0),B(0,1,0),D( ,
,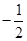 ,0),F(0,0,1),
,0),F(0,0,1),
∴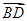 =(
=( ,
,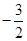 ,0),
,0),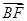 ==(0,?1,1),
==(0,?1,1),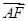 =(-
=(- ,0,1),
,0,1),
设平面BDF的一个法向量为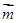 =(x,y,z),则
=(x,y,z),则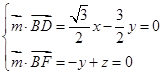 ,取z=1,则
,取z=1,则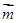 =(
=( ,1,1),
,1,1),
所以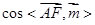 =
=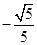 ,∴直线AF与面BDF所成角的余弦值为
,∴直线AF与面BDF所成角的余弦值为 . (12分)
. (12分)
考点:空间线面垂直的判定,空间面面垂直的判定,线面角的计算,推理论证能力,运算求解能力

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
 ,则
,则 不可能与
不可能与 内无数条直线相交。
内无数条直线相交。 中,
中, ,
, 平面
平面 ,
, 为
为 的中点,
的中点, ,
, .
. ;
; 为
为 的中点,求证:平面
的中点,求证:平面 平面
平面 .
.
 为斜三棱柱
为斜三棱柱 的侧棱
的侧棱 上一点,
上一点,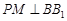 交
交 于点
于点 ,
, 交
交 于点
于点 .
.
 ;
; 中有余弦定理:
中有余弦定理: .
. -A BC中,AB
-A BC中,AB 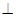 AC, AB=AC=2,
AC, AB=AC=2,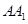 =4,点D是BC的中点.
=4,点D是BC的中点.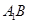 与
与 所成角的余弦值;
所成角的余弦值; 与
与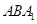 所成二面角的正弦值.
所成二面角的正弦值.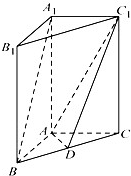

 ,那么b与c夹角是
,那么b与c夹角是 
 与平面
与平面 相交,直线
相交,直线 是平面
是平面 ,则直线
,则直线