题目内容
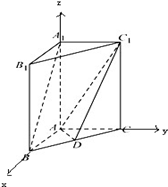
如图,在直三棱柱中 -A BC中,AB
-A BC中,AB 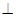 AC, AB=AC=2,
AC, AB=AC=2,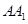 =4,点D是BC的中点.
=4,点D是BC的中点.
(1)求异面直线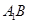 与
与 所成角的余弦值;
所成角的余弦值;
(2)求平面 与
与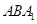 所成二面角的正弦值.
所成二面角的正弦值.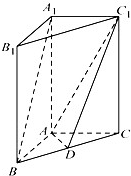
解析试题分析:(1)以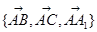 为单位正交基底建立空间直角坐标系
为单位正交基底建立空间直角坐标系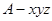 ,利用向量法能求出异面直线
,利用向量法能求出异面直线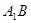 与
与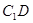 所成角的余弦值;(2)分别求出平面
所成角的余弦值;(2)分别求出平面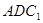 的法向量与
的法向量与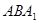 的法向量,利用法向量能求出平面
的法向量,利用法向量能求出平面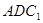 与
与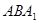 所成二面角的余弦值,再由三角函数知识能求出平面
所成二面角的余弦值,再由三角函数知识能求出平面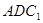 与
与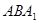 所成二面角的正弦值.
所成二面角的正弦值.
试题解析:(1)以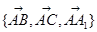 为单位正交基底建立空间直角坐标系
为单位正交基底建立空间直角坐标系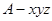 ,
,
则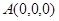 ,
,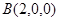 ,
,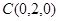 ,
,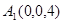 ,
,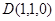 ,
,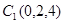 .
.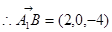 ,
,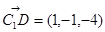
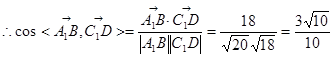
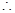 异面直线
异面直线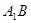 与
与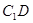 所成角的余弦值为
所成角的余弦值为 .
.
(2) 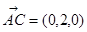 是平面
是平面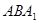 的的一个法向量,设平面
的的一个法向量,设平面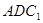 的法向量为
的法向量为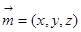 ,
,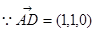 ,
,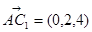 ,
,
由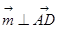 ,
,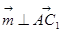 得
得 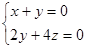 ,取
,取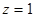 ,得
,得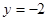 ,
,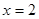 ,
,
所以平面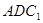 的法向量为
的法向量为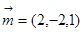 .
.
设平面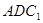 与
与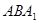 所成二面角为
所成二面角为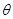 .
.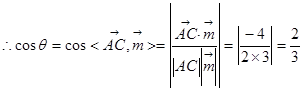 , 得
, 得 .
.
所以平面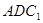 与
与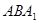 所成二面角的正弦值为
所成二面角的正弦值为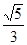 .
.
考点:与二面角有关的立体几何综合题;异面直线及其所成的角.

练习册系列答案
相关题目
 ,FC
,FC  平面ABCD, AE
平面ABCD, AE 
 ,且AC=BC.
,且AC=BC. 平面EBC;
平面EBC; 的大小.
的大小.

 平面
平面 ,且四边形
,且四边形 ,
, ,
, ,
, .
.
 平面
平面 ;(2)求平面
;(2)求平面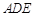 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.

 中,底面
中,底面 是矩形,
是矩形,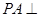 平面
平面 ,
, ,
, 依次是
依次是 的中点.
的中点.
 ;
; 与平面
与平面 所成角的正弦值.
所成角的正弦值. 中,
中, 为矩形,平面
为矩形,平面 平面
平面

 问
问 为何值时,四棱锥
为何值时,四棱锥 与平面
与平面 夹角的余弦值.
夹角的余弦值.
 上移动,其中a,b,c为某一直角三角形的三条边长,c为斜边,则m2+n2的最小值是 .
上移动,其中a,b,c为某一直角三角形的三条边长,c为斜边,则m2+n2的最小值是 .