题目内容
如图,点 为斜三棱柱
为斜三棱柱 的侧棱
的侧棱 上一点,
上一点,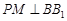 交
交 于点
于点 ,
, 交
交 于点
于点 .
.
(1) 求证: ;
;
(2) 在任意 中有余弦定理:
中有余弦定理: .
.
拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明
(1)见解析 (2) 见解析
解析试题分析:(1)由题意和三棱柱的性质,证出 CC1⊥平面PMN,再证 CC1⊥MN.
(2)利用类比推理边“对应侧面面积”得出结论,证明用到余弦定理平行四边形的面积公式和题中的垂直关系.
试题解析:(1) 证: ;(4分)
;(4分)
(2) 解:在斜三棱柱 中,有
中,有 ,其中
,其中 为平面
为平面 与平面
与平面 所组成的二面角.
所组成的二面角. 上述的二面角为
上述的二面角为 ,在
,在 中,
中,
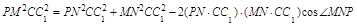 ,
,
由于 ,
,
∴有 (12分)
(12分)
考点:空间中直线与直线之间的位置关系;归纳推理.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 ,FC
,FC  平面ABCD, AE
平面ABCD, AE 
 中,
中, ,
, ,
,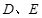 分别为
分别为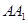 和
和 的中点.
的中点.

 平面
平面 ;(5分)
;(5分) 的体积.(7分)
的体积.(7分) ,且AC=BC.
,且AC=BC. 平面EBC;
平面EBC; 的大小.
的大小.

 平面
平面 ,且四边形
,且四边形 ,
, ,
, ,
, .
.
 平面
平面 ;(2)求平面
;(2)求平面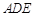 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.
 中,底面
中,底面 是矩形,
是矩形,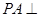 平面
平面 ,
, ,
, 依次是
依次是 的中点.
的中点.
 ;
; 与平面
与平面 所成角的正弦值.
所成角的正弦值. 和
和 所在平面互相垂直,且
所在平面互相垂直,且 ,
, ,E、F、G分别为AC、DC、AD的中点.
,E、F、G分别为AC、DC、AD的中点. 平面BCG;
平面BCG; ,其中S为底面面积,h为高.
,其中S为底面面积,h为高.
 直线
直线 的距离是
的距离是  中,
中, ,它所在平面外一点
,它所在平面外一点 到
到 的距离是 .
的距离是 .