题目内容
(本小题满分12分)
若盒中装有同一型号的灯泡共10只,其中有8只合格品,2只次品。
(Ⅰ)某工人师傅有放回地连续从该盒中取灯泡3次,每次取一只灯泡,求2次取到次品的概率;
(Ⅱ)某工人师傅用该盒中的灯泡去更换会议室的一只已坏灯泡,每次从中取一灯泡,若是正品则用它更换已坏灯泡,若是次品则将其报废(不再放回原盒中),求成功更换会议室的已坏灯泡所用灯泡只数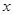 的分布列和数学期望。
的分布列和数学期望。
(Ⅰ)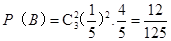 ;
;
(Ⅱ)X的分布列如下表:X 1 2 3 p 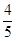
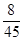
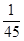
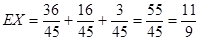 。
。
解析试题分析:(Ⅰ)设一次取次品记为事件A,由古典概型概率公式得: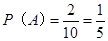 ….(2分)
….(2分)
有放回连续取3次,其中2次取得次品记为事件B,由独立重复试验得: 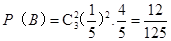 …………………………………..(5分)
…………………………………..(5分)
(Ⅱ)依据知X的可能取值为1.2.3 …………..(6分)
且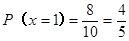 ……………..(7分)
……………..(7分) …………………..(8分)
…………………..(8分)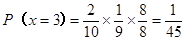 ………………………..(9分)
………………………..(9分)
则X的分布列如下表:
…………………..(10分) X 1 2 3 p 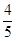
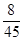
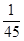
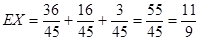 …………………………………..(12分)
…………………………………..(12分)
考点:本题主要考查离散性随机变量的分布列及期望。
点评:典型题,利用概率知识解决实际问题,在高考题中常常出现,这类题目解答的难点在于求随机变量的概率。本题涉及古典概型概率计算,独立重复试验概率计算,注意运用公式。

练习册系列答案
相关题目
 ,遇到红灯时停留的时间都是2 分钟. 设这名学生在路上遇到红灯的个数为变量
,遇到红灯时停留的时间都是2 分钟. 设这名学生在路上遇到红灯的个数为变量 、停留的总时间为变量
、停留的总时间为变量 ,
, .
. ,且各题回答正确与否相互之间没有影响.
,且各题回答正确与否相互之间没有影响. 分,负者得
分,负者得 分,比赛进行到有一人比对方多
分,比赛进行到有一人比对方多 分或打满
分或打满 局时结束.假设选手甲与选手乙比赛时,甲每局获胜的概率皆为
局时结束.假设选手甲与选手乙比赛时,甲每局获胜的概率皆为 ,且各局比赛胜负互不影响.
,且各局比赛胜负互不影响. 局结束,且乙比甲多得
局结束,且乙比甲多得 表示比赛停止时已比赛的局数,求随机变量
表示比赛停止时已比赛的局数,求随机变量 的分布列和数学期望;
的分布列和数学期望; (
(
 )
) 从集合
从集合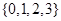 中任取一个元素,
中任取一个元素, 从集合
从集合 恰有两个不相等实根的概率;
恰有两个不相等实根的概率; 中任取一个数,
中任取一个数, 中任取一个数,求方程
中任取一个数,求方程 个等级,等级系数
个等级,等级系数 依次为
依次为 ,其中
,其中 为标准
为标准 ,
, 为标准
为标准 ,产品的等级系数越大表明产品的质量越好,已知某厂执行标准
,产品的等级系数越大表明产品的质量越好,已知某厂执行标准 件,相应的等级系数组成一个样本,数据如下:
件,相应的等级系数组成一个样本,数据如下: 的为一等品,等级系数
的为一等品,等级系数 的为二等品,等级系数
的为二等品,等级系数 的为三等品,
的为三等品, ,从该厂生产的产品中任取一件,其利润记为
,从该厂生产的产品中任取一件,其利润记为 ,用这个样本的频率分布估计总体分布,将频率视为概率,求
,用这个样本的频率分布估计总体分布,将频率视为概率,求