题目内容
(本题满分12分)一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4,
(Ⅰ)从袋中随机取出两个球,求取出的球的编号之和不大于4的概率;
(Ⅱ)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,求n<m+2的概率。
(1)1/3
(2)13/16
解析试题分析:解:(I)从袋子中随机取两个球,其一切可能的结果组成的基本事件有1和2,1和3,1和4,2和3,2和4,3和4,共6个。
从袋中随机取出的球的编号之和不大于4的事件共有1和2,1和3两个。
因此所求事件的概率为1/3。
(II)先从袋中随机取一个球,记下编号为m,放回后,在从袋中随机取一个球,记下编号为n,其一切可能的结果(m, n)有:
(1,1)(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1)(3,2), (3,3) (3,4),(4,1) (4,2),(4,3)(4,4),共16个
有满足条件n≥ m+2 的事件为(1,3) (1,4) (2,4),共3个
所以满足条件n ≥ m+2 的事件的概率为 P=3/16
故满足条件n<m+2 的事件的概率为13/16
考点:古典概型
点评:解决该试题的关键是对于试验基本空间的理解和准确的求解运用,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
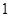 次,求在这一枪出现空弹的概率;
次,求在这一枪出现空弹的概率; 次,求在这三枪中出现空弹的概率
次,求在这三枪中出现空弹的概率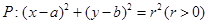 被y轴所截的弦长为2,被x轴分成两段弧,且弧长之比等于
被y轴所截的弦长为2,被x轴分成两段弧,且弧长之比等于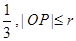 (其中
(其中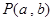 为圆心,O为坐标原点)。
为圆心,O为坐标原点)。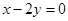 上的投影为A,求事件“在圆P内随机地投入一点,使这一点恰好在
上的投影为A,求事件“在圆P内随机地投入一点,使这一点恰好在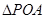 内”的概率的最大值
内”的概率的最大值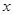 的分布列和数学期望。
的分布列和数学期望。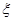 个球,求
个球,求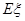 。
。