题目内容
某学生在上学路上要经过4个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是 ,遇到红灯时停留的时间都是2 分钟. 设这名学生在路上遇到红灯的个数为变量
,遇到红灯时停留的时间都是2 分钟. 设这名学生在路上遇到红灯的个数为变量 、停留的总时间为变量
、停留的总时间为变量 ,
,
(1)求这名学生在上学路上到第三个路口时首次遇到红灯的概率;
(2)这名学生在上学路上遇到红灯的个数至多是2个的概率.
(3)求 的标准差
的标准差 .
.
(1)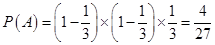
(2)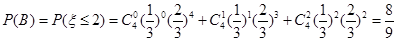
(3)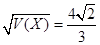
解析试题分析:解(1)设这名学生在上学路上到第三个路口时首次遇到红灯为事件A,因为事件A等于事件“这名学生在第一和第二个路口没有遇到红灯,在第三个路口遇到红灯”,所以事件A的概率为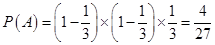 4分
4分
(2)设这名学生在上学路遇到红灯的个数至多是2个为事件B,这名学生在上学路上遇到红灯的个数 ~
~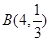 .
.
则由题意:
∴这名学生在上学路遇到红灯的个数至多是2个的概率为 . 10分
. 10分
(3)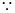
 ~
~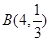 ,∴
,∴ , 12分
, 12分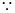
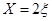 ,∴
,∴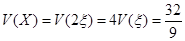 ,
,
∴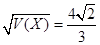 14分
14分
考点:二项分布
点评:主要是考查了独立事件的概率以及二项分布的期望值和方差的求解运用,属于中档题。

练习册系列答案
相关题目

 ,乙射击一次中靶概率是
,乙射击一次中靶概率是 ,
,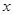 的分布列和数学期望。
的分布列和数学期望。