题目内容
如图,在正三棱柱ABC-A1B1C1中,点D在边BC上, AD⊥C1D.
 (Ⅰ)求证:AD⊥平面BC C1 B1;
(Ⅰ)求证:AD⊥平面BC C1 B1;
(Ⅱ)设E是B1C1上的一点,当 的值为多少时,
的值为多少时,
A1E∥平面ADC1?请给出证明.
【答案】
解: (Ⅰ)在正三棱柱中,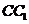 ⊥平面
⊥平面 ,
,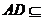 平面
平面 ,
,
∴ 。 ………………………………………2分
。 ………………………………………2分
又 ,
,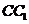 交
交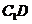 于
于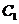 ,且
,且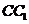 和
和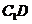 都在面
都在面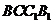 内,
内,
∴ . ………………………………………5分(Ⅱ)由(1),得
. ………………………………………5分(Ⅱ)由(1),得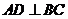 .在正三角形
.在正三角形 中,D是BC的中点.…………7分
中,D是BC的中点.…………7分
当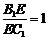 ,即E为
,即E为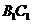 的中点时,
的中点时,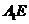 ∥平面
∥平面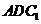 .………………8分
.………………8分
事实上,正三棱柱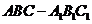 中,四边形
中,四边形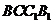 是矩形,且D、E分别是
是矩形,且D、E分别是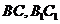 的中点,所以
的中点,所以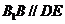 且
且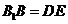 .…………………10分
.…………………10分
又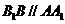 ,且
,且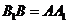 ,
,
∴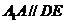 ,且
,且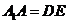 . ………………………………………12分
. ………………………………………12分
所以四边形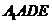 为平行四边形,所以
为平行四边形,所以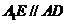 .
.
而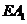 在平面
在平面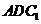 外,故
外,故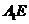 ∥平面
∥平面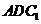 .
………………………14分
.
………………………14分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在正三棱柱ABC-A1B1C1中,AB=1,若二面角C-AB-C1的大小为60°,则点C到平面C1AB的距离为( )
如图,在正三棱柱ABC-A1B1C1中,AB=1,若二面角C-AB-C1的大小为60°,则点C到平面C1AB的距离为( )A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
 如图,在正三棱柱ABC-A1B1C1中,D、E、G分别是AB、BB1、AC1的中点,AB=BB1=2.
如图,在正三棱柱ABC-A1B1C1中,D、E、G分别是AB、BB1、AC1的中点,AB=BB1=2. 如图,在正三棱柱ABC-A1B1C1中,AA1=4,AB=2,M是AC的中点,点N在AA1上,
如图,在正三棱柱ABC-A1B1C1中,AA1=4,AB=2,M是AC的中点,点N在AA1上, (2012•马鞍山二模)如图,在正三棱柱ABC一DEF中,AB=2,AD=1,P是CF的延长线上一点,过A、B、P三点的平面交FD于M,交EF于N.
(2012•马鞍山二模)如图,在正三棱柱ABC一DEF中,AB=2,AD=1,P是CF的延长线上一点,过A、B、P三点的平面交FD于M,交EF于N.