题目内容
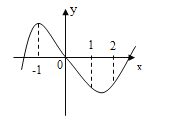
【题目】已知函数![]() 的图象如图所示,则
的图象如图所示,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】由图象可知:经过原点,∴f(0)=0=d,
∴![]() .
.
由图象可得:函数f(x)在[1,1]上单调递减,函数f(x)在x=1处取得极大值。
∴f′(x)=3ax2+2bx+c0在[1,1]上恒成立,且f′(1)=0.
得到3a2b+c=0,即c=2b3a,
∵f′(1)=3a+2b+c<0,
∴4b<0,即b<0,
∵f′(2)=12a+4b+c>0,
∴3a+2b>0,
设k=![]() ,则k=
,则k=![]() ,
,
建立如图所示的坐标系,则点A(1,2),
则k=![]() 式中变量a、b满足下列条件
式中变量a、b满足下列条件![]() ,
,
作出可行域如图:
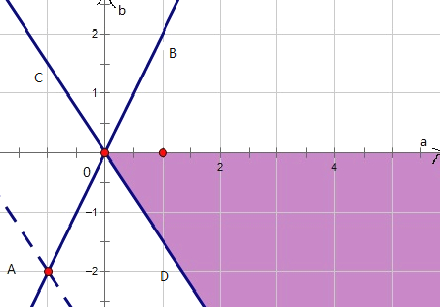
∴k的最大值就是kAB=![]() ,k的最小值就是kCD,而kCD就是直线3a+2b=0的斜率,kCD=
,k的最小值就是kCD,而kCD就是直线3a+2b=0的斜率,kCD=![]() ,
,
∴![]() <k<
<k<![]() .
.
∴故选D.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
【题目】某校举行汉字听写比赛,为了了解本次比赛成绩情况,从得分不低于50分的试卷中随机抽取100名学生的成绩(得分均为整数,满分100分)进行统计,请根据频率分布表中所提供的数据,解答下列问题:
组号 | 分组 | 频数 | 频率 |
第1组 | [50,60) | 5 | 0.05 |
第2组 | [60,70) |
| 0.35 |
第3组 | [70,80) | 30 |
|
第4组 | [80,90) | 20 | 0.20 |
第5组 | [90,100] | 10 | 0.10 |
合计 | 100 | 1.00 |
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若从成绩较好的第3、4、5组中按分层抽样的方法抽取6人参加市汉字听写比赛,并从中选出2人做种子选手,求2人中至少有1人是第4组的概率。