题目内容
某公司招聘员工采取两次考试(笔试)的方法：第一试考选择题，共10道题（均为四选一题型），每题10分，共100分；第二试考解答题，共3题。规则是：只有在一试中达到或超过80分者才获通过并有资格参加二试，参加二试的人只有答对2题或3题才能被录用。现有甲、乙两人参加该公司的招聘考试。且已知在一试时：两人均会做10道题中的6道；对于另外4道题来说，甲有两题可排除两个错误答案、有两题完全要猜，乙有两题可排除一个错误答案、有一题可排除两个错误答案、有一题完全要猜。进入二试后，对于任意一题，甲答对的概率是
、乙答对的概率是
.（1）分别求甲、乙两人能通过一试进入二试的概率
、
；（2）求甲、乙两人都能被录用的概率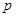
.
(1)
， 
；（2）甲、乙都能被录取的概率是
.
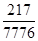解析试题分析：(1)两人都已稳得60分，另外至少还要得20分，所以只需考虑另外4个.这4个题中答对2个或3个或4 个均可进入第二轮，三种情况的概率相加即得.也可以求出不能进入第二轮的概率，用1减去这个概率即得能进入二轮的概率.
（2）分别求出甲、乙能被录取的概率相乘即得甲、乙都能被录取的概率.
试题解析：(1)据条件有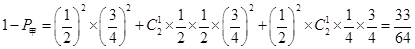
，所以 4分
同理 6分
（2）甲能被录取的概率是
8分
乙能被录取的概率是
10分
所以甲、乙都能被录取的概率是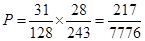
12分
考点：古典概型.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
,乙获胜的概率为
,现已赛完两局,乙暂时以2∶0领先.某学校的三个学生社团的人数分布如下表（每名学生只能参加一个社团）：
| | 围棋社 | 舞蹈社 | 拳击社 |
| 男生 | 5 | 10 | 28 |
| 女生 | 15 | 30 | m |
（Ⅰ）求拳击社团被抽出的6人中有5人是男生的概率；
（Ⅱ）设拳击社团有X名女生被抽出，求X的分布列及数学期望
. 
顶点
起跳，每步从一顶点跳到相邻的顶点．
的概率
；
表示跳到过
．
.
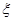，试写出
,
；
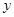人,求这2人都来自高二年级的概率.
，甲、丙两人都回答错误的概率是
，乙、丙两人都回答正确的概率是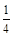
.
表示回答该题正确的人数，求
.
，
.
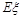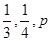的值，