题目内容
甲、乙两名教师进行乒乓球比赛,采用七局四胜制(先胜四局者获胜).若每一局比赛甲获胜的概率为 ,乙获胜的概率为
,乙获胜的概率为 ,现已赛完两局,乙暂时以2∶0领先.
,现已赛完两局,乙暂时以2∶0领先.
(1)求甲获得这次比赛胜利的概率;
(2)设比赛结束时比赛的局数为随机变量X,求随机变量X的概率分布和数学期望EX.
(1) 甲获得这次比赛胜利的概率为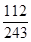 ;(2) X的概率分布为:
;(2) X的概率分布为:X 4 5 6 7 P ? 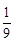
? 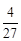
? 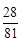
? 
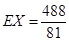 .
.
解析试题分析:(1)甲获得这次比赛胜利情况有二,一是比赛六局结束,甲连续赢了四局,一是比赛了七局,甲在后五局中赢了四局,且最后一局是甲赢,显然这两种情况彼此互斥,故分别计算出这两个事件的概率,求其和即得甲获得这次比赛胜利的概率.(2)设比赛结束时比赛的局数为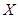 ,由题意得随机变量
,由题意得随机变量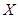 可能的取值为4,5,6,7,分别求出随机变量
可能的取值为4,5,6,7,分别求出随机变量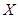 的概率,从而得分布列和数学期望.本题考查
的概率,从而得分布列和数学期望.本题考查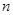 次独立重复试验中恰好发生
次独立重复试验中恰好发生 次的概率,解题的关键是正确理解两个事件、“甲获得这次比赛胜利”,再由概率的计算公式计算出概率.本题是概率中的有一定综合性的题,对事件正确理解与分类是很关键.
次的概率,解题的关键是正确理解两个事件、“甲获得这次比赛胜利”,再由概率的计算公式计算出概率.本题是概率中的有一定综合性的题,对事件正确理解与分类是很关键.
试题解析:(1)设甲获胜为事件A,则甲获胜包括甲以4∶2获胜和甲以4∶3获胜两种情况.
设甲以4∶2获胜为事件A1,则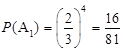 2分
2分
设甲以4∶3获胜为事件A2,则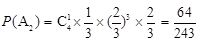 5分
5分
P(A)=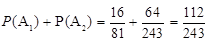 . 6分
. 6分
(2)随机变量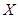 可能的取值为4,5,6,7,
可能的取值为4,5,6,7,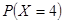 =
=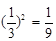 .
.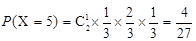 .
. .
.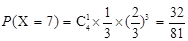 .
.
X的概率分布为:X 4 5 6 7 P ? 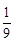
? 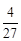
? 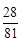
? 
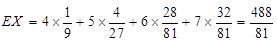 12分
12分
考点:离散型随机变量及其分布列;相互独立事件的概率乘法公式;离散型随机变量的期望与方差.

在一次数学测验后,班级学委对选答题的选题情况进行了统计,如下表:
| | 几何证明选讲 | 坐标系与 参数方程 | 不等式选讲 | 合计 |
| 男同学(人数) | 12 | 4 | 6 | 22 |
| 女同学(人数) | 0 | 8 | 12 | 20 |
| 合计 | 12 | 12 | 18 | 42 |
| | 几何类 | 代数类 | 总计 |
| 男同学(人数) | 16 | 6 | 22 |
| 女同学(人数) | 8 | 12 | 20 |
| 总计 | 24 | 18 | 42 |
(2)在原统计结果中,如果不考虑性别因素,按分层抽样的方法从选做不同选做题的同学中随机选出7名同学进行座谈.已知这名班级学委和两名数学科代表都在选做“不等式选讲”的同学中.
①求在这名班级学委被选中的条件下,两名数学科代表也被选中的概率;
②记抽到数学科代表的人数为X,求X的分布列及数学期望E(X).
下面临界值表仅供参考:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |

某牛奶厂要将一批牛奶用汽车从所在城市甲运至城市乙,已知从城市甲到城市乙只有两条公路,且运费由厂商承担.若厂商恰能在约定日期(×月×日)将牛奶送到,则城市乙的销售商一次性支付给牛奶厂20万元;若在约定日期前送到,每提前一天销售商将多支付给牛奶厂1万元;若在约定日期后送到,每迟到一天销售商将少支付给牛奶厂1万元.为保证牛奶新鲜度,汽车只能在约定日期的前两天出发,且只能选择其中的一条公路运送牛奶,已知下表内的信息:
| 统计信息 汽车行驶路线 | 在不堵车的情况下到达城市乙所需时间(天) | 在堵车的情况下到达城市乙所需时间(天) | 堵车的概率 | 运费(万元) |
| 公路1 | 2 | 3 | 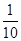 | 1.6 |
| 公路2 | 1 | 4 | 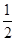 | 0.8 |
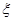 (单位:万元),求
(单位:万元),求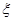 的分布列和数学期望
的分布列和数学期望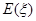 ;
;(II)如果你是牛奶厂的决策者,你选择哪条公路运送牛奶有可能让牛奶厂获得的毛收入更多?
(注:毛收入=销售商支付给牛奶厂的费用-运费)
生产A,B两种元件,其质量按测试指标划分为:指标大于或等于82为正品,小于82为
次品,现随机抽取这两种元件各100件进行检测,检测结果统计如下:
| 测试指标 | 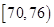 | 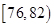 | 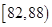 | 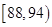 | 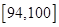 |
| 元件A | 8 | 12 | 40 | 32 | 8 |
| 元件B | 7 | 18 | 40 | 29 | 6 |
(Ⅱ)生产一件元件A,若是正品可盈利50元,若是次品则亏损10元;生产一件元件B,若是正品可盈利100元,若是次品则亏损20元,在(Ⅰ)的前提下;
(i)求生产5件元件B所获得的利润不少于300元的概率;
(ii)记X为生产1件元件A和1件元件B所得的总利润,求随机变量X的分布列和数学期望.
 ,科目B每次考试成绩合格的概率均为
,科目B每次考试成绩合格的概率均为 .假设各次考试成绩合格与否均互不影响.
.假设各次考试成绩合格与否均互不影响. ,求
,求 、乙答对的概率是
、乙答对的概率是 .(1)分别求甲、乙两人能通过一试进入二试的概率
.(1)分别求甲、乙两人能通过一试进入二试的概率 、
、 ;(2)求甲、乙两人都能被录用的概率
;(2)求甲、乙两人都能被录用的概率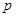 .
.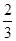 .
.