题目内容
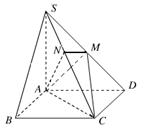
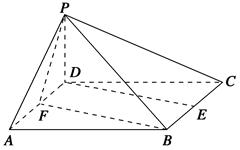
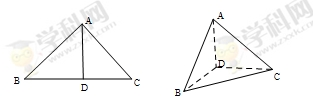
如图,在四棱锥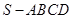 中,底面
中,底面 是正方形,
是正方形,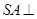 底面
底面 ,
, ,点
,点 是
是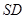 的中点,
的中点,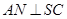 ,交
,交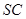 于点
于点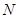 .
.
(1)求证:平面 平面
平面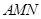 ;
;
(2)求三棱锥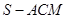 的体积.
的体积.
(1)详见解析;(2)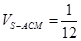 .
.
解析试题分析:(1)求证:平面 平面
平面 ,证明两个平面垂直,只需证明一个平面过另一个平面的垂线即可,注意到已知
,证明两个平面垂直,只需证明一个平面过另一个平面的垂线即可,注意到已知 ,可想到证明
,可想到证明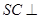 面
面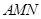 ,只需证明
,只需证明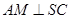 ,或
,或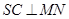 ,但
,但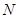 位置不确定,可考虑证
位置不确定,可考虑证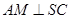 ,由已知点
,由已知点 是
是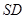 的中点,已知
的中点,已知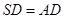 ,故
,故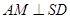 ,而四棱锥
,而四棱锥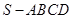 的底面
的底面 是正方形,
是正方形,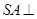 底面
底面 ,故
,故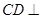 面
面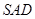 ,这样能得到
,这样能得到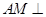 面
面 ,从而得
,从而得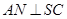 ,问题得证;(2)求三棱锥
,问题得证;(2)求三棱锥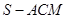 的体积,由于
的体积,由于 是
是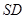 的中点,则
的中点,则 ,这样转化为求
,这样转化为求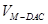 ,由图可知,
,由图可知,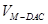 容易求出.
容易求出.
试题解析:(1)∵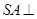 底面
底面 ,∴
,∴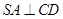
又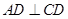 ∴
∴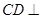 面
面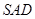
∴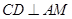 ······① 3分
······① 3分
又 ,且
,且 是
是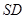 的中点,∴
的中点,∴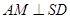 ·········②
·········②
由①②得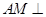 面
面 ∴
∴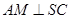
又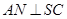 ∴
∴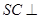 面
面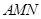
∴平面 平面
平面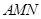 6分
6分
(2)∵ 是
是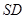 的中点,∴
的中点,∴ . 9分
. 9分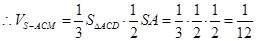 12分
12分
考点:面面垂直,几何体的体积.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
 .
.
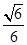 ,求四棱锥PABCD的体积.
,求四棱锥PABCD的体积. ,DC⊥平面ABC,EB⊥平面ABC, AB=AC=BE=2,CD=1。
,DC⊥平面ABC,EB⊥平面ABC, AB=AC=BE=2,CD=1。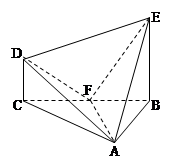
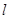 ,求证:
,求证: 中,
中, ,
, ,
,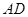 是
是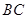 上的高,沿
上的高,沿 折起,使
折起,使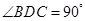 .
.
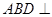 平面
平面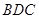 ;
;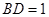 ,求三棱锥
,求三棱锥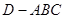 的体积.
的体积.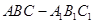 中,四边形
中,四边形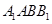 为菱形,
为菱形,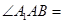
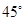 ,四边形
,四边形 为矩形,若
为矩形,若 ,
, ,
, .
.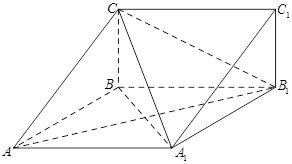
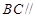 平面
平面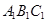 ;
;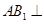 面
面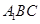 ;
;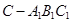 的体积.
的体积.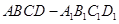 中,
中,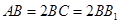 , 沿平面
, 沿平面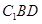 把这个长方体截成两个几何体: 几何体(1);几何体(2)
把这个长方体截成两个几何体: 几何体(1);几何体(2)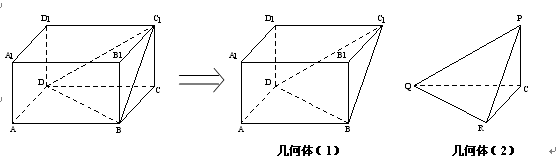
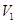 、
、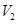 ,求
,求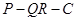 的正切值
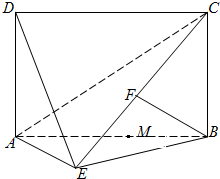
的正切值 为矩形,
为矩形, 平面
平面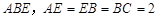 ,
,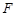 为
为 上的点,且
上的点,且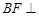 平面
平面 .
. 
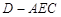 的体积;
的体积;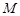 在线段
在线段 上,且满足
上,且满足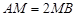 ,试在线段
,试在线段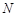 ,使得
,使得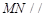 平面
平面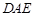 .
.